题目内容
(本小题满分14分)
椭圆 过点P
过点P ,且离心率为
,且离心率为 ,F为椭圆的右焦点,
,F为椭圆的右焦点, 、
、 两点在椭圆
两点在椭圆 上,且
上,且  ,定点
,定点 (-4,0).
(-4,0).

(Ⅰ)求椭圆C的方程;
(Ⅱ)当 时 ,问:MN与AF是否垂直;并证明你的结论.
时 ,问:MN与AF是否垂直;并证明你的结论.
(Ⅲ)当 、
、 两点在
两点在 上运动,且
上运动,且 =6
=6 时
时 , 求直线MN的方程.
, 求直线MN的方程.
椭圆
 过点P
过点P ,且离心率为
,且离心率为 ,F为椭圆的右焦点,
,F为椭圆的右焦点, 、
、 两点在椭圆
两点在椭圆 上,且
上,且  ,定点
,定点 (-4,0).
(-4,0).
(Ⅰ)求椭圆C的方程;
(Ⅱ)当
 时 ,问:MN与AF是否垂直;并证明你的结论.
时 ,问:MN与AF是否垂直;并证明你的结论.(Ⅲ)当
 、
、 两点在
两点在 上运动,且
上运动,且 =6
=6 时
时 , 求直线MN的方程.
, 求直线MN的方程.解:(Ⅰ)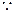 椭圆的离心率为
椭圆的离心率为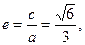
即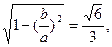 可得
可得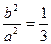
 --2分
--2分
又椭圆 过点P
过点P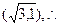
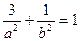
解得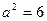 ,
,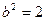 ,椭圆C的方程为
,椭圆C的方程为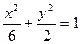 -----
-----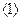 -----------4分
-----------4分
(Ⅱ)设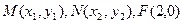 ,
,
则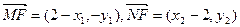 ,
,
当 时,
时,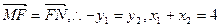 , -----------5分
, -----------5分
由M,N两点在椭圆上,
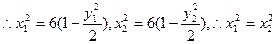 ---------6分
---------6分
若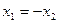 ,则
,则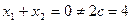 (舍去),
(舍去), ------------7分
------------7分
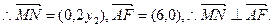 . ------------8分
. ------------8分
(Ⅲ)因为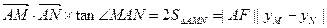 =6
=6 .--9分
.--9分
由已知点F(2,0), 所以|AF|="6, " 即得|yM-yN|=
 ------------10分
------------10分
当MN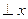 轴时,
轴时,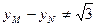 故直线的斜率存在. ------------11分
故直线的斜率存在. ------------11分
不妨设直线MN的方程为: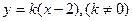 -----
-----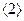
联立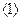 、
、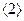 得
得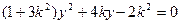
 ------------12分
------------12分
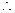 |
|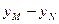 |=
|=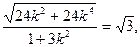 解得
解得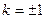 ------------14分
------------14分
此时,直线MN的方程为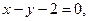 或
或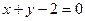 ------------15分
------------15分
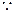 椭圆的离心率为
椭圆的离心率为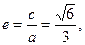
即
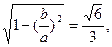 可得
可得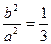
 --2分
--2分又椭圆
 过点P
过点P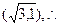
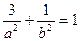
解得
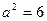 ,
,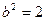 ,椭圆C的方程为
,椭圆C的方程为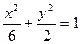 -----
-----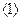 -----------4分
-----------4分(Ⅱ)设
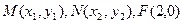 ,
,则
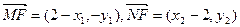 ,
, 当
 时,
时,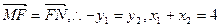 , -----------5分
, -----------5分由M,N两点在椭圆上,
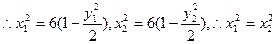 ---------6分
---------6分若
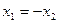 ,则
,则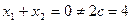 (舍去),
(舍去), ------------7分
------------7分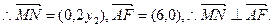 . ------------8分
. ------------8分(Ⅲ)因为
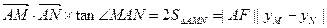 =6
=6 .--9分
.--9分由已知点F(2,0), 所以|AF|="6, " 即得|yM-yN|=

 ------------10分
------------10分当MN
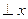 轴时,
轴时,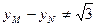 故直线的斜率存在. ------------11分
故直线的斜率存在. ------------11分不妨设直线MN的方程为:
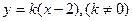 -----
-----
联立
 、
、 得
得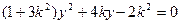
 ------------12分
------------12分 |
|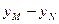 |=
|=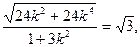 解得
解得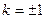 ------------14分
------------14分此时,直线MN的方程为
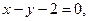 或
或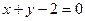 ------------15分
------------15分略

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 、
、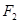 是椭圆
是椭圆 的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足
的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足 为坐标原点),
为坐标原点), ,若椭圆的离心率等于
,若椭圆的离心率等于
 的面积等于
的面积等于 ,求椭圆的方程;
,求椭圆的方程; 的面积等于
的面积等于 ?若存在,求出点M的坐标;若不存在,说明理由.
?若存在,求出点M的坐标;若不存在,说明理由.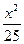 +
+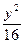 =1上任意一点,F1、F2为左、右焦点,如图所示.
=1上任意一点,F1、F2为左、右焦点,如图所示.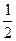 |PF1|;
|PF1|;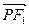 ·
·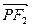 =0,若存在,求出P点的坐标, 若不存在,试说明理由
=0,若存在,求出P点的坐标, 若不存在,试说明理由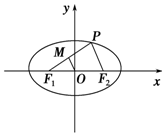
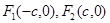 是椭圆
是椭圆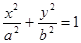
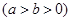 的两个焦点,
的两个焦点,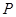 是以
是以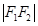 为直径的圆与椭圆的一个交点,且
为直径的圆与椭圆的一个交点,且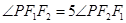 ,则该椭圆的离心率为 ( )
,则该椭圆的离心率为 ( )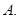 .
.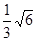
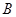 .
.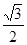
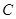 .
.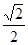
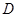 .
.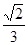
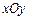 中,点
中,点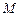 到点
到点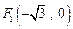 ,
,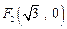 的距离之和是
的距离之和是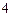 ,点
,点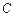 ,直线
,直线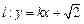 与轨迹
与轨迹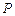 和
和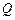 .⑴求轨迹
.⑴求轨迹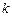 ,
,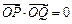 ?若存在,求出
?若存在,求出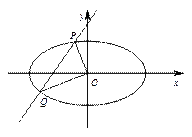
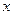 轴上,中心在坐标原点的椭圆C的离心率为
轴上,中心在坐标原点的椭圆C的离心率为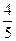 ,且过点
,且过点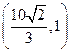 (题干自编)
(题干自编)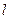 分别切椭圆C与圆
分别切椭圆C与圆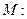
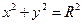 (其中
(其中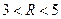 )于
)于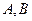 两点,求
两点,求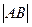 的最大值。
的最大值。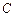 :
: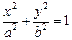 (
(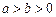 ),其焦距为
),其焦距为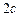 ,若
,若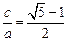 (
(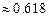 ),则称椭圆
),则称椭圆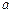 、
、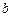 、
、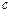 成等比数列.
成等比数列.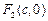 ,
,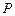 为椭圆
为椭圆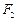 、
、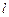 ,使
,使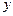 轴的交点
轴的交点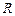 满足
满足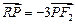 ?若存在,求直线
?若存在,求直线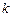 ;若不存在,请说明理由.
;若不存在,请说明理由.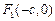 、
、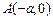 、
、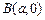 、
、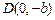 、
、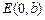 为顶点的菱形
为顶点的菱形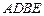 的内切圆过焦点
的内切圆过焦点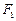 、
、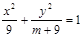 的离心率为
的离心率为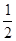 ,则m= ( )
,则m= ( )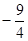
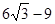
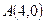
 和
和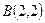 ,
,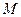 是椭圆
是椭圆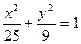 上一动点,则
上一动点,则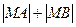 的最大值是____________
的最大值是____________