题目内容
已知三角形ABC的三个顶点均在椭圆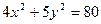 上,且点A是椭圆短轴的一个端点(点A在y轴正半轴上).
上,且点A是椭圆短轴的一个端点(点A在y轴正半轴上).
(1)若三角形ABC的重心是椭圆的右焦点,试求直线BC的方程;若角A为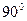 ,AD垂直BC于D,试求点D的轨迹方程.
,AD垂直BC于D,试求点D的轨迹方程.
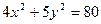 上,且点A是椭圆短轴的一个端点(点A在y轴正半轴上).
上,且点A是椭圆短轴的一个端点(点A在y轴正半轴上).(1)若三角形ABC的重心是椭圆的右焦点,试求直线BC的方程;若角A为
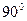 ,AD垂直BC于D,试求点D的轨迹方程.
,AD垂直BC于D,试求点D的轨迹方程.所求点D的轨迹方程是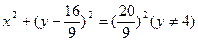
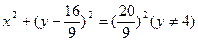
1)设B(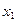 ,
,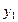 ),C(
),C(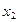 ,
,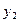
 ),BC中点为(
),BC中点为(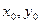 ),F(2,0)
),F(2,0)
则有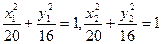
两式作差有
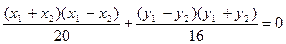

 (1)
(1)
F(2,0)为三角形重心,所以由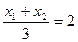 ,得
,得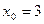
由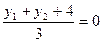 得
得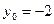 ,
,
代入(1)得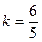
直线BC的方程为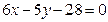
2)由AB⊥AC得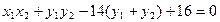 (2)
(2)
设直线BC方程为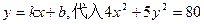 ,得
,得
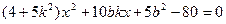
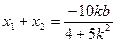 ,
,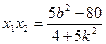
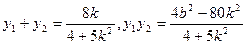 代入(2)式得
代入(2)式得
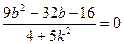 ,解得
,解得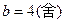 或
或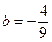
直线过定点(0,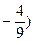 ,设D(x,y)
,设D(x,y)
则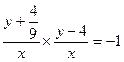
即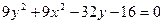
所以所求点D的轨迹方程是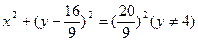 。
。
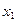 ,
,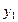 ),C(
),C(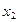 ,
,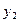
 ),BC中点为(
),BC中点为(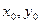 ),F(2,0)
),F(2,0)则有
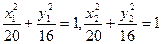
两式作差有
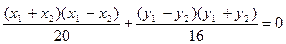

 (1)
(1)F(2,0)为三角形重心,所以由
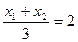 ,得
,得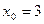
由
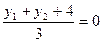 得
得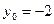 ,
,代入(1)得
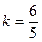
直线BC的方程为
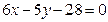
2)由AB⊥AC得
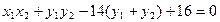 (2)
(2)设直线BC方程为
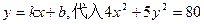 ,得
,得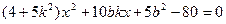
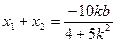 ,
,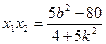
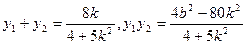 代入(2)式得
代入(2)式得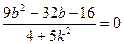 ,解得
,解得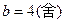 或
或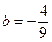
直线过定点(0,
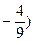 ,设D(x,y)
,设D(x,y)则
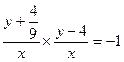
即
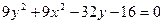
所以所求点D的轨迹方程是
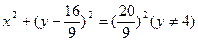 。
。
练习册系列答案
相关题目
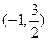 ;
;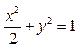 ,
,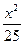 +
+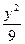 ="1"
="1"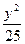 +
+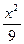 =1(y≠0)
=1(y≠0)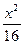 +
+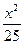 +
+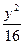 =1上一点,则
=1上一点,则 x+
x+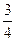 y的最小值为__________________.
y的最小值为__________________.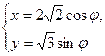 (φ为参数)上一点M与原点的连线与x轴正方向所成角为
(φ为参数)上一点M与原点的连线与x轴正方向所成角为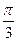 ,求点M的坐标.
,求点M的坐标.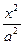 +
+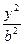 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=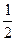 ,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D,则tan∠BDC的值等于( )
,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D,则tan∠BDC的值等于( )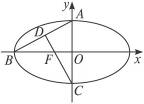
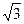 B.-3
B.-3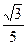 D.-
D.-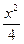 +y2=1相交于A、B两点,则|AB|的最大值是( )
+y2=1相交于A、B两点,则|AB|的最大值是( )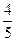
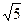 C.
C.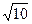 D.
D.