题目内容
8．已知0＜α＜$\frac{π}{2}$，求证：sinα+cosα＞1．分析 作出三角函数线，由三角形两边之和大于第三边可得结论．
解答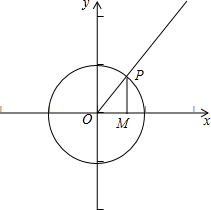 
证明：如图P为α与单位圆交点，
则OP=1，OM、MP分别为α的余弦线，正弦线，
由三角形两边之和大于第三边可得OM+MP＞OP，
即sinα+cosα＞1
点评 本题考查三角函数线，属基础题．
练习册系列答案
相关题目
13．向量$\overrightarrow{a}$=（1，3），$\overrightarrow{b}$=（2，4），$\overrightarrow{c}$=$\overrightarrow{a}$+λ$\overrightarrow{b}$，$\overrightarrow{d}$=λ$\overrightarrow{a}$-$\overrightarrow{b}$，若$\overrightarrow{c}$⊥$\overrightarrow{d}$，则λ的值为（ ）
| A． | $\frac{1±5\sqrt{2}}{7}$ | B． | $\frac{5±\sqrt{221}}{14}$ | C． | ±1 | D． | 以上A、B、C均不对 |
6．已知椭圆的左焦点为F1，右焦点为F2．若椭圆上存在一点P，满足线段PF2相切于以椭圆的短轴为直径的圆，切点为线段PF2的中点，则该椭圆的离心率为（ ）
| A． | $\frac{{\sqrt{5}}}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{{\sqrt{3}}}{6}$ | D． | $\frac{{\sqrt{2}}}{3}$ |