题目内容
12.已知$\frac{3π}{4}$<α<π,tanα+$\frac{1}{tanα}$=-$\frac{10}{3}$.(1)求tanα的值;
(2)求$\frac{si{n}^{2}(π+α)+2sinαsin(\frac{π}{2}+α)+1}{3sinαcos(\frac{π}{2}-α)-2cosαcos(π-α)}$的值.
分析 (1)由条件解方程求得tanα的值,再根据α的范围,进一步确定tanα的值.
(2)由条件利用 诱导公式、同角三角函数的基本关系,求得所给式子的值.
解答 解:(1)因为tan α+$\frac{1}{tanα}$=-$\frac{10}{3}$,所以3tan2α+10tan α+3=0,
解得tan α=-$\frac{1}{3}$或tan α=-3.
因为$\frac{3π}{4}$<α<π,所以-1<tanα<0,所以tanα=-$\frac{1}{3}$.
(2)原式=$\frac{{sin}^{2}α+2sinαcosα+1}{{3sin}^{2}α+{2cos}^{2}α}$=$\frac{{2sin}^{2}α+2sinαcosα{+cos}^{2}α}{{3sin}^{2}α+{2cos}^{2}α}$=$\frac{{2tan}^{2}α+2tanα+1}{{3tan}^{2}α+2}$=$\frac{5}{21}$.
点评 本题主要考查同角三角函数的基本关系、诱导公式的应用,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
相关题目
4.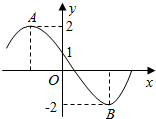 函数f(x)=2sin(ωx+φ)的部分图象如图所示,其中A,B两点之间的距离为5,那么下列说法正确的是( )
函数f(x)=2sin(ωx+φ)的部分图象如图所示,其中A,B两点之间的距离为5,那么下列说法正确的是( )
 函数f(x)=2sin(ωx+φ)的部分图象如图所示,其中A,B两点之间的距离为5,那么下列说法正确的是( )
函数f(x)=2sin(ωx+φ)的部分图象如图所示,其中A,B两点之间的距离为5,那么下列说法正确的是( )| A. | 函数f(x)的最小正周期为8 | |
| B. | f(3)=-$\frac{1}{2}$ | |
| C. | x=$\frac{3}{2}$是函数f(x)的一条对称轴 | |
| D. | 函数f(x)向右平移一个单位长度后所得的函数为偶函数 |
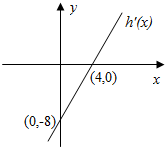 已知二次函数h(x)=ax2+bx+2,其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).
已知二次函数h(x)=ax2+bx+2,其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).