Question

【题目】已知函数，，则的零点个数为( )

A. 6B. 7C. 8D. 9

Answer 1

【答案】B

【解析】

利用复合函数的性质，转化为新的方程x3﹣9x＝10或13或7的解的问题，然后转化为交点问题即可得答案．

根据题意得，若函数f（x）＝x3﹣9x＝0x（x2﹣9）＝0，解得x＝0或±3；

令g（x）＝f（f（x）﹣10）＝0f（x）﹣10＝0或±3，即x3﹣9x＝10或13或7；

∵f（x）＝x3﹣9x，∴f′（x）＝3x2﹣9＝3（x2﹣3）；

令f′（x）＝0x＝±；令f′（x）＞0x或x；令f′（x）＜0；

且f（）；f（）＝﹣；

画出函数f（x）草图为：

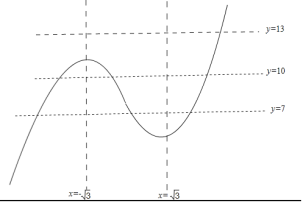
通过图象可以发现：x2﹣9x＝10或13或7共有7个解，

故函数g（x）有7个零点．

故选：B．