题目内容
【题目】已知直线
，抛物线C：
上一动点P到直线
和
轴距离之和的最小值是（ ）
A.1B.2C.
D.
【答案】A
【解析】
抛物线
上一动点P到直线
和
轴距离之和最小转化为：抛物线上一动点P到直线和直线x＝-1的距离之和最小，x＝1是抛物线的准线，则P到x＝1的距离等于PF，F（1，0）为抛物线的焦点，过F作
垂线，和抛物线的交点就是P，所以点P到直线
的距离和到轴的距离之和的最小值就是F（1，0）到直线距离再减1．
解：x＝1是抛物线的准线，抛物线的焦点F（1，0），
则P到x＝1的距离等于PF，
过F作垂线，和抛物线的交点就是P，
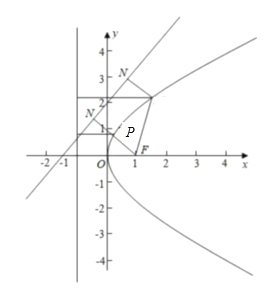
所以点P到直线：的距离和到直线：x＝1的距离之和的最小值
就是F（1，0）到直线距离，
所以最小值
．
抛物线上一动点P到直线和轴的距离之和的最小值是：21＝1
故选：A．
练习册系列答案
名校课堂系列答案
相关题目
