题目内容
【题目】平面直角坐标系中,![]() 为坐标原点,射线
为坐标原点,射线![]() 与
与![]() 轴正半轴重合,射线
轴正半轴重合,射线![]() 在第一象限,且与
在第一象限,且与![]() 轴正半轴的夹角为
轴正半轴的夹角为![]() ,在
,在![]() 上有点列
上有点列![]() ,在
,在![]() 上有点
上有点![]() ,已知
,已知![]() ,
,![]()
(1)求点![]() 和
和![]() 的坐标;
的坐标;
(2)求![]() 的坐标;
的坐标;
(3)求![]() 面积的最大值,并求出此时的
面积的最大值,并求出此时的![]() 值.
值.
【答案】(1)点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() (2)
(2)![]() 的坐标为
的坐标为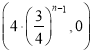 ,
,![]() 的坐标为
的坐标为![]() (3)
(3)![]() 的面积最大为
的面积最大为![]() ,此时
,此时![]() 或
或![]() .
.
【解析】
(1)由![]() 和
和![]() 即可求出点
即可求出点![]() 的坐标,由射线
的坐标,由射线![]() 在第一象限,且与
在第一象限,且与![]() 轴正半轴的夹角为
轴正半轴的夹角为![]() ,
,![]() 可求出
可求出![]() ;
;
(2)设![]() ,则可由
,则可由![]() 得到
得到![]() ,根据等比数列的知识即可求出
,根据等比数列的知识即可求出![]() 的坐标,由
的坐标,由![]() 以及等差数列知识可求出
以及等差数列知识可求出![]() ,再根据三角函数的定义即可求出
,再根据三角函数的定义即可求出![]() 的坐标;
的坐标;
(3)由![]() 的坐标分别求出
的坐标分别求出![]() ,再根据三角形的面积公式即可表示出
,再根据三角形的面积公式即可表示出![]() 面积,再判断该式的单调性即可求出最大值以及此时的
面积,再判断该式的单调性即可求出最大值以及此时的![]() 值.
值.
(1)由![]() 得,
得,![]() ,因为
,因为![]() ,所以
,所以![]() ,即点
,即点![]() 的坐标为
的坐标为![]() .
.
由射线![]() 在第一象限,且与
在第一象限,且与![]() 轴正半轴的夹角为
轴正半轴的夹角为![]() ,
,![]() ,根据三角函数的定义可知,点
,根据三角函数的定义可知,点![]() 的坐标为
的坐标为![]() 即
即![]() .
.
(2)设![]() ,则可由
,则可由![]() 得到
得到![]() ,所以
,所以![]() 为等比数列,
为等比数列,
![]() ,故
,故![]() 的坐标为
的坐标为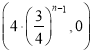 .
.
由![]() 可知,
可知,![]() 为等差数列,因为
为等差数列,因为![]() ,所以
,所以![]() ,
,
三角函数的定义即可求出![]() 的坐标为
的坐标为![]() 即
即![]() .
.
(3)由![]() 的坐标为
的坐标为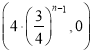 ,
,![]() 的坐标为
的坐标为![]() ,所以
,所以![]()
![]() ,
,![]() 的面积为
的面积为![]() ,
,
设![]() ,令
,令 ,解得
,解得![]() ,
,
所以![]() ,故
,故![]() 的面积最大为
的面积最大为![]() ,此时
,此时![]() 或
或![]() .
.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目