题目内容
设函数f(x)=ax+cosx,x∈[0,π]。
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)设f(x)≤1+sinx,求a的取值范围。
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)设f(x)≤1+sinx,求a的取值范围。
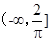
【命题意图】本试题考查了导数在研究函数中的运用。第一就是函数中有三角函数,要利用三角函数的有界性,求解单调区间。另外就是运用导数证明不等式问题的构造函数思想的运用。
【点评】试题分为两问,题面比较简单,给出的函数比较新颖,因为里面还有三角函数,,这一点对于同学们来说比较有点难度,不同于平时的练习,相对来说比较做的少。但是解决的关键还是要看导数的符号的实质不变,求解单调区间。第二问中,运用构造函数的思想,证明不等式,一直以来是个难点,那么这类问题的关键是找到合适的函数,来运用导数证明最值问题大于零或者小于零得到解决。

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
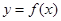 对任意的实数
对任意的实数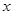 ,都有
,都有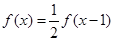 ,且当
,且当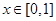 时,
时,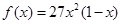 。
。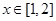 时,求
时,求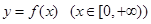 ,试问:在它的图象上是否存在点
,试问:在它的图象上是否存在点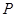 ,使得函数在点
,使得函数在点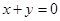 平行。若存在,那么这样的点
平行。若存在,那么这样的点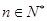 ,且
,且 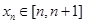 ,记
,记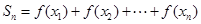 ,求证:
,求证: 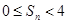 。
。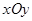 中,
中,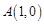 、
、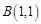 、
、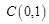 ,映射
,映射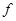 将
将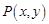 对应到另一个平面直角坐标系
对应到另一个平面直角坐标系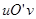 上的点
上的点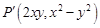 ,则当点
,则当点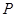 沿着折线
沿着折线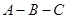 运动时,在映射
运动时,在映射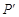 的轨迹是( )
的轨迹是( )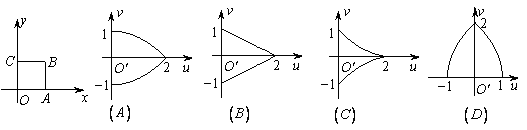
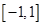 上存在零点,求实数p的取值范围;
上存在零点,求实数p的取值范围; 的值域为区间
的值域为区间 ,且
,且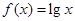 ,若
,若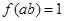 ,则
,则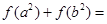
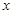 (
(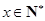 )件.当
)件.当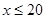 时,年销售总收入为(
时,年销售总收入为(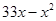 )万元;当
)万元;当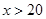 时,年销售总收入为260万元.记该工厂生产并销售这种产品所得的年利润为
时,年销售总收入为260万元.记该工厂生产并销售这种产品所得的年利润为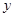 万元,则
万元,则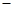 年总投资)
年总投资)
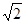 是函数
是函数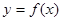 的极值点,其中
的极值点,其中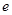 是自然对数的底数.
是自然对数的底数.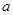 的值;
的值;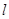 同时满足:
同时满足: 处的切线,
处的切线,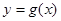 的图象相切于点
的图象相切于点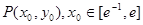 .
.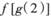 的值为
的值为