题目内容
7.在△ABC中,已知下列条件,解三角形(边长精确到1cm):(1)A=70°,C=30°,c=20 cm;
(2)A=34°,B=56°,c=68 cm.
分析 (1)通过A=70°、C=30°及三角形内角和定理可知B=80°,利用正弦定理分别能求出另两边的长度;
(2)通过A=34°、B=56°及三角形内角和定理可知C=90°,利用正弦定理分别能求出另两边的长度.
解答 解:(1)∵A=70°,C=30°,
∴B=180°-(A+C)=180°-(70°+30°)=80°,
又∵c=20cm,
∴a=c•$\frac{sinA}{sinC}$=20•$\frac{sin70°}{sin30°}$=40sin70°≈38cm,
b=c•$\frac{sinB}{sinC}$=20•$\frac{sin80°}{sin30°}$=40sin80°≈39cm;
(2)∵A=34°,B=56°,
∴C=180°-(A+B)=180°-(34°+56°)=90°,
又∵c=68cm,
∴a=c•$\frac{sinA}{sinC}$=68•$\frac{sin34°}{sin90°}$=68sin34°≈38cm,
b=c•$\frac{sinB}{sinC}$=68•$\frac{sin56°}{sin90°}$=68sin56°≈56cm.
点评 本题考查解三角形,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
17.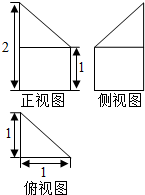 若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( )
若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( )
 若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( )
若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( )| A. | $\frac{2}{3}$cm3 | B. | $\frac{1}{3}$cm3 | C. | 1cm3 | D. | 2cm3 |
16.已知集合M是由a=x2-y2,x,y∈N得到所有a值组成的,对于元素6和7,( )
| A. | 仅有7∈M | B. | 仅有6∈M | C. | 都属于M | D. | 都不属于M |
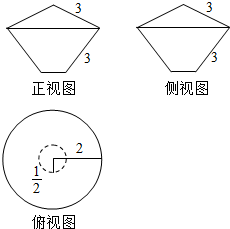 根据几何图的表面积(如图所示),求该几何体的表面积.
根据几何图的表面积(如图所示),求该几何体的表面积.