题目内容
如图,在长方体ABCD-A1B1C1D1中,点E、F分别BB1、DD1上,且AE⊥A1B,AF⊥A1D.(1)求证:A1C⊥平面AEF;
(2)若规定两个平面所成的角是这两个平面所组成的二面角中的锐角(或直角),则在空间中有定理:若两条直线分别垂直于两个平面,则这两条直线所成的角与这两个平面所成的角相等.
试根据上述定理,在AB=4,AD=3,AA1=5时,求平面AEF与平面D1B1BD所成的角的大小.(用反三角函数值表示)
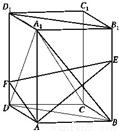
【答案】分析:(1)这一问中寻找垂直关系的方法是典型的三垂线定理的应用,三垂线定理是证明异面直线垂直的常用的方法,尤其在正方体、长方体中,与它们的体对角线相关联的时候,经常用到.
(2)这一问如果要作出平面AEF与平面D1B1BD所成的平面角的话,辅助线过多,难度系数较大.但是如果把它放到空间直角坐标系去解决,就轻松多了.依托长方体自身的好条件,分别以AB、AD、AA1为x轴、y轴、z轴建立空间坐标系.这样解的好处就是:(1)解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理,因为这些可以用向量方法来解决.(2)即使立体感稍差一些的学生也可以顺利解出,因为只需画个草图以建立坐标系和观察有关点的位置即可.
解答: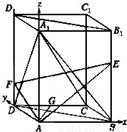 证明:(1)如图,因为CB⊥平面A1B,所A1C在平面A1B上的射影为A1B
证明:(1)如图,因为CB⊥平面A1B,所A1C在平面A1B上的射影为A1B
由A1B⊥AE,AE?平面A1B,得A1C⊥AE,
同理可证A1C⊥AF
因为A1C⊥AF,A1C⊥AE
所以A1C⊥平面AEF
解:(2)过A作BD的垂线交CD于G,
因为D1D⊥AG,所以AG⊥平面D1B1BD
设AG与A1C所成的角为α,则α即为平面AEF与平面D1B1BD所成的角.
由已知,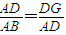 计算得
计算得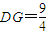 .
.
如图建立直角坐标系,则得点A(0,0,0),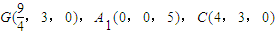 ,
,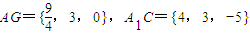 ,
,
因为AG与A1C所成的角为α
所以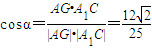
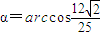
由定理知,平面AEF与平面CEF所成角的大小为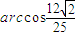
点评:本小题主要考查空间线面关系、三垂线定理的应用、构造空间直角坐标系,设定参数,运用向量等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.
(2)这一问如果要作出平面AEF与平面D1B1BD所成的平面角的话,辅助线过多,难度系数较大.但是如果把它放到空间直角坐标系去解决,就轻松多了.依托长方体自身的好条件,分别以AB、AD、AA1为x轴、y轴、z轴建立空间坐标系.这样解的好处就是:(1)解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理,因为这些可以用向量方法来解决.(2)即使立体感稍差一些的学生也可以顺利解出,因为只需画个草图以建立坐标系和观察有关点的位置即可.
解答:
 证明:(1)如图,因为CB⊥平面A1B,所A1C在平面A1B上的射影为A1B
证明:(1)如图,因为CB⊥平面A1B,所A1C在平面A1B上的射影为A1B由A1B⊥AE,AE?平面A1B,得A1C⊥AE,
同理可证A1C⊥AF
因为A1C⊥AF,A1C⊥AE
所以A1C⊥平面AEF
解:(2)过A作BD的垂线交CD于G,
因为D1D⊥AG,所以AG⊥平面D1B1BD
设AG与A1C所成的角为α,则α即为平面AEF与平面D1B1BD所成的角.
由已知,
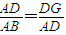 计算得
计算得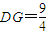 .
.如图建立直角坐标系,则得点A(0,0,0),
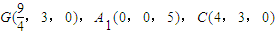 ,
,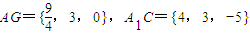 ,
,因为AG与A1C所成的角为α
所以
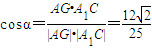
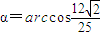
由定理知,平面AEF与平面CEF所成角的大小为
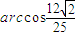
点评:本小题主要考查空间线面关系、三垂线定理的应用、构造空间直角坐标系,设定参数,运用向量等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为:
如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为: 如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )
如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )

 .
. 
 ,AA1 =
,AA1 = ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.