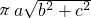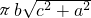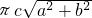题目内容
 如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )
如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )分析:得当ABCD在圆柱的底面上时,由题意可得圆柱的高等于c,直径2r=
,故外接圆柱侧面积为 2πrc=πc
,同理求的当ABB1A1在圆柱的底面上以及当BCC1B1在圆柱的底面上时,外接圆柱侧面积,在这三个侧面积中找出最小的即为所求.
| a2+b2 |
| a2+b2 |
解答:解:当ABCD在圆柱的底面上时,由题意可得AC等于圆柱的底面直径2r,圆柱的高等于c.
故2r=
,故外接圆柱侧面积为 2πrc=πc
.
同理可得,当ABB1A1在圆柱的底面上时,外接圆柱侧面积为 πb
;
当BCC1B1在圆柱的底面上时,外接圆柱侧面积为 πa
.
令a=3,b=2,c=1,检验可得在 πc
、πb
、πa
中,最小的是πc
.
故选:C.
故2r=
| a2+b2 |
| a2+b2 |
同理可得,当ABB1A1在圆柱的底面上时,外接圆柱侧面积为 πb
| a2+c2 |
当BCC1B1在圆柱的底面上时,外接圆柱侧面积为 πa
| b2+c2 |
令a=3,b=2,c=1,检验可得在 πc
| a2+b2 |
| a2+c2 |
| b2+c2 |
| a2+b2 |
故选:C.
点评:本题主要考查圆柱体的侧面积公式,求出圆柱底面的半径,是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
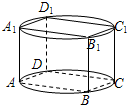 如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于
如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于