��Ŀ����
���Ŀ���������������14�֣���ͼ���ڳ�����
ABCD��A1B1C1D1�У�AD=AA1=1��AB=2����E����AB���ƶ�.
��1��֤����D1E��A1D;
��2����EΪAB���е�ʱ�����E����ACD1�ľ��룻
��3��AE���ں�ֵʱ�������D1��EC��D�Ĵ�СΪ .��������������������������������������������
.��������������������������������������������

����������(��������14��)
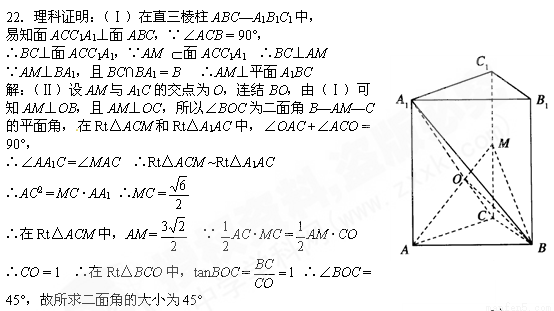
��ͼ����ֱ������ABC �C A1B1C1�У���ACB = 90�㣬CB = 1��
CA = ��AA1 =
��AA1 = ��MΪ����CC1��һ�㣬AM��BA1��
��MΪ����CC1��һ�㣬AM��BA1��
������֤��AM��ƽ��A1BC��
����������B �C AM �C C�Ĵ�С��
�������C��ƽ��ABM�ľ��룮

�����ģ��ⷨһ��1����AE��ƽ��AA1DD1��A1D��AD1����D1E��A1D��
��2�����E����ACD1�ľ���Ϊh���ڡ�ACD1�У�AC=CD1=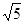 ��AD1=
��AD1=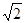 ����
����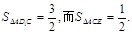
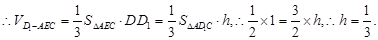
��3����D��DH��CE��H����D1H��DE����D1H��CE�����DHD1Ϊ�����D1��EC��D��ƽ���.��AE=x����BE=2��x��
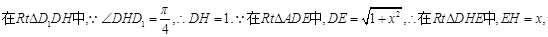

 ��3����ƽ��D1EC�ķ�����
��3����ƽ��D1EC�ķ�����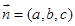 ��
��
��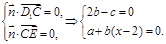 ��b=1,
��c=2,a=2��x����
��b=1,
��c=2,a=2��x����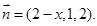 ������
������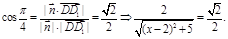 ��
�� �����ϣ���ȥ����
�����ϣ���ȥ����
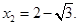 ��AE=
��AE=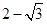 ʱ�������D1��EC��D�Ĵ�СΪ
ʱ�������D1��EC��D�Ĵ�СΪ .
.
 �������C��ƽ��ABM�ľ���Ϊh����֪BO =
�������C��ƽ��ABM�ľ���Ϊh����֪BO =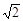 ����֪S��ABM =
����֪S��ABM = �� AM �� BO =
�� AM �� BO = ��
�� ��VC �C ABM = VM �C ABC ��
��VC �C ABM = VM �C ABC �� hS��ABM
=
hS��ABM
= MC
��S��ABC
MC
��S��ABC
��h =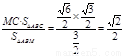 ���C��ƽ��ABM�ľ���Ϊ
���C��ƽ��ABM�ľ���Ϊ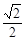 �ⷨ��������ͬ�ⷨһ
�ⷨ��������ͬ�ⷨһ
������ͼ��CΪԭ�㣬CA��CB��CC1����ֱ��
�ֱ�Ϊx�ᣬy�ᣬz�ᣬ�����ռ�ֱ������ϵ��
��A (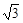 ��0��0)��A1(
��0��0)��A1(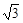 ��0��
��0��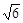 )��B (0��1��0)��
)��B (0��1��0)��
��M (0��0��z1) ��AM��BA1��
��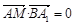 �����C 3 + 0 +
�����C 3 + 0 +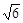 z1 = 0����z1 =
z1 = 0����z1 =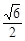 ������M (0��0��
������M (0��0��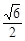 )
)
������m = (x��y��z)Ϊƽ��AMB�ķ���������m��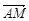 ��m��
��m�� ����
����
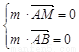 ��
��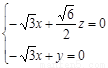 ����x = 1��ƽ��AMB��һ��������Ϊm = (1��
����x = 1��ƽ��AMB��һ��������Ϊm = (1��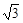 ��
��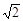 )����Ȼ����
)����Ȼ����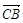 ��ƽ��AMC��һ��������
��ƽ��AMC��һ��������
cos < m��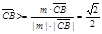 ����֪��m��
����֪��m��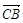 ���еĽǵ��ڶ����B��AM��C�Ĵ�С�����������ǵĴ�СΪ45�㣮 �����������Ϊ��
���еĽǵ��ڶ����B��AM��C�Ĵ�С�����������ǵĴ�СΪ45�㣮 �����������Ϊ��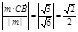 �� ����C��ƽ��ABM�ľ���Ϊ
�� ����C��ƽ��ABM�ľ���Ϊ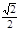
����������

 ����ν����Ž̲��㽭���̴�ѧ������ϵ�д�
����ν����Ž̲��㽭���̴�ѧ������ϵ�д� �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�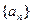 �������ʽ
�������ʽ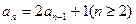 ������
������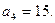
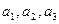 ��
�� ��������
��������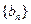 ��
��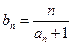 ������
������ ��ǰn���
��ǰn���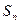 .
.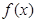 �Ķ�����ϵ��Ϊ
�Ķ�����ϵ��Ϊ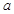 ���Ҳ���ʽ
���Ҳ���ʽ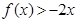 �Ľ⼯Ϊ
�Ľ⼯Ϊ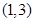 ��
��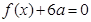 ��������ȵ�ʵ����, ��
��������ȵ�ʵ����, �� �������ʽ
�������ʽ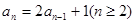 ������
������
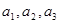 ��
�� ��������
��������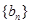 ��
�� ������
������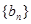 ��ǰn���
��ǰn��� .
.