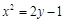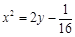题目内容
抛物线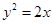 上的两点
上的两点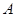 、
、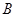 到焦点的距离之和是
到焦点的距离之和是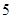 ,则线段
,则线段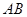 的中点到
的中点到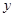 轴的距离是 .
轴的距离是 .
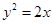 上的两点
上的两点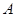 、
、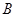 到焦点的距离之和是
到焦点的距离之和是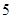 ,则线段
,则线段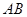 的中点到
的中点到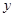 轴的距离是 .
轴的距离是 .2
试题分析:根据抛物线的方程求出准线方程,利用抛物线的定义抛物线上的点到焦点的距离等于到准线的距离,列出方程求出A,B的中点横坐标,求出线段AB的中点到y轴的距离解:∵F是抛物线y2=2x的焦点F(
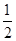 ,0)准线方程x=-
,0)准线方程x=-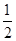 设A(x1,y1) B(x2,y2),∴|AF|+|BF|=x1+
设A(x1,y1) B(x2,y2),∴|AF|+|BF|=x1+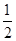 +x2+
+x2+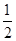 =5,解得x1+x2=4,∴线段AB的中点横坐标为:2.故线段
=5,解得x1+x2=4,∴线段AB的中点横坐标为:2.故线段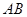 的中点到
的中点到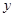 轴的距离是2.答案为:2
轴的距离是2.答案为:2点评:本题考查抛物线的基本性质,利用抛物线的定义将到焦点的距离转化为到准线的距离是解题的关键

练习册系列答案
相关题目
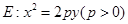 的焦点F作斜率分别为
的焦点F作斜率分别为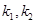 的两条不同的直线
的两条不同的直线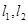 ,且
,且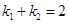 ,
,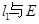 相交于点A,B,
相交于点A,B,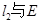 相交于点C,D。以AB,CD为直径的圆M,圆N(M,N为圆心)的公共弦所在的直线记为
相交于点C,D。以AB,CD为直径的圆M,圆N(M,N为圆心)的公共弦所在的直线记为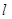 。
。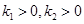 ,证明;
,证明;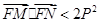 ;
;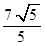 ,求抛物线E的方程。
,求抛物线E的方程。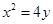 的焦点为
的焦点为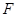 ,准线与y轴的交点为
,准线与y轴的交点为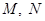 为抛物线上的一点,且满足
为抛物线上的一点,且满足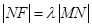 ,则
,则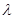 的取值范围是 ____ .
的取值范围是 ____ .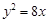 上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是( )
上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是( )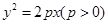 上,另一个顶点
上,另一个顶点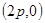 ,这样的正三角形有( )
,这样的正三角形有( )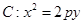 (
(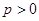 )上一点
)上一点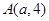 到其准线的距离为
到其准线的距离为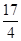 .
.
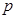 与
与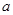 的值;
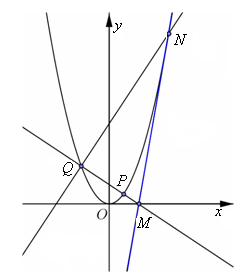
的值;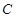 上动点
上动点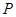 的横坐标为
的横坐标为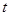 (
(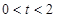 ),过点
),过点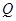 ,交
,交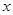 轴于
轴于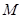 点(直线
点(直线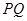 的斜率记作
的斜率记作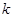 ).过点
).过点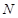 .若
.若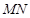 恰好是
恰好是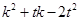 是否为定值?若是,求出该定值;若不是,说明理由.
是否为定值?若是,求出该定值;若不是,说明理由.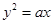 的焦点到准线的距离为4,则此抛物线的焦点坐标为
的焦点到准线的距离为4,则此抛物线的焦点坐标为


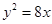 上一点P到y轴的距离是4,则点P到该抛物线的焦点的距离是 ( )
上一点P到y轴的距离是4,则点P到该抛物线的焦点的距离是 ( )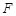 是抛物线
是抛物线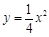 的焦点,
的焦点,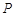 是该抛物线上的动点,则线段
是该抛物线上的动点,则线段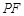 中点的轨迹方程是( )
中点的轨迹方程是( )