题目内容
设椭圆C: =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,右焦点到直线
,右焦点到直线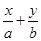 =1的距离d=
=1的距离d=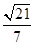 ,O为坐标原点.
,O为坐标原点.
(1)求椭圆C的方程;
(2)过点O作两条互相垂直的射线,与椭圆C分别交于A,B两点,证明,点O到直线AB的距离为定值,并求弦AB长度的最小值.
 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,右焦点到直线
,右焦点到直线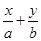 =1的距离d=
=1的距离d=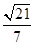 ,O为坐标原点.
,O为坐标原点.(1)求椭圆C的方程;
(2)过点O作两条互相垂直的射线,与椭圆C分别交于A,B两点,证明,点O到直线AB的距离为定值,并求弦AB长度的最小值.
(1)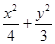 =1(2)
=1(2)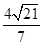
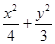 =1(2)
=1(2)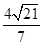
(1)由e= 得
得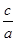 =
= ,即a=2c,∴b=
,即a=2c,∴b= c.
c.
由右焦点到直线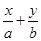 =1的距离为d=
=1的距离为d=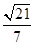 ,
,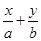 =1化为一般式:bx+ay-ab=0得
=1化为一般式:bx+ay-ab=0得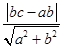 =
=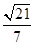 ,解得a=2,b=
,解得a=2,b= .
.
所以椭圆C的方程为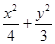 =1.
=1.
(2)设A(x1,y1),B(x2,y2),当直线AB斜率存在时,设直线AB的方程为y=kx+m.与椭圆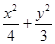 =1联立消去y,得(4k2+3)x2+8kmx+(4m2-12)=0.由根与系数的关系得x1+x2=-
=1联立消去y,得(4k2+3)x2+8kmx+(4m2-12)=0.由根与系数的关系得x1+x2=-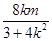 ,x1x2=
,x1x2=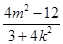 .
.
∵OA⊥OB,∴x1x2+y1y2=0,∴x1x2+(kx1+m)(kx2+m)=0,即(k2+1)x1x2+km(x1+x2)+m2=0,
∴(k2+1)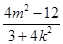 -
-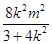 +m2=0.
+m2=0.
整理得7m2=12(k2+1),所以O到直线AB的距离d=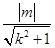 =
= =
=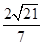 (为定值).
(为定值).
当直线AB斜率不存在时,可求出直线AB方程为x=±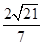 ,则点O到直线AB的距离为
,则点O到直线AB的距离为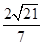 (定值)
(定值)
∵OA⊥OB,∴OA2+OB2=AB2≥2OA·OB,当且仅当OA=OB时取“=”,由直角三角形面积公式得:
d·AB=OA·OB.
∵OA·OB≤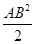 ,∴d·AB≤
,∴d·AB≤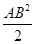 .
.
∴AB≥2d=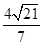 ,故当OA=OB时,弦AB的长度取得最小值
,故当OA=OB时,弦AB的长度取得最小值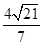 .
.
 得
得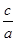 =
= ,即a=2c,∴b=
,即a=2c,∴b= c.
c.由右焦点到直线
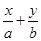 =1的距离为d=
=1的距离为d=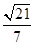 ,
,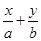 =1化为一般式:bx+ay-ab=0得
=1化为一般式:bx+ay-ab=0得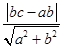 =
=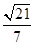 ,解得a=2,b=
,解得a=2,b= .
.所以椭圆C的方程为
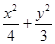 =1.
=1.(2)设A(x1,y1),B(x2,y2),当直线AB斜率存在时,设直线AB的方程为y=kx+m.与椭圆
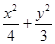 =1联立消去y,得(4k2+3)x2+8kmx+(4m2-12)=0.由根与系数的关系得x1+x2=-
=1联立消去y,得(4k2+3)x2+8kmx+(4m2-12)=0.由根与系数的关系得x1+x2=-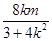 ,x1x2=
,x1x2=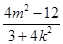 .
.∵OA⊥OB,∴x1x2+y1y2=0,∴x1x2+(kx1+m)(kx2+m)=0,即(k2+1)x1x2+km(x1+x2)+m2=0,
∴(k2+1)
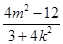 -
-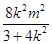 +m2=0.
+m2=0.整理得7m2=12(k2+1),所以O到直线AB的距离d=
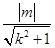 =
= =
=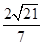 (为定值).
(为定值).当直线AB斜率不存在时,可求出直线AB方程为x=±
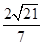 ,则点O到直线AB的距离为
,则点O到直线AB的距离为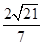 (定值)
(定值)∵OA⊥OB,∴OA2+OB2=AB2≥2OA·OB,当且仅当OA=OB时取“=”,由直角三角形面积公式得:
d·AB=OA·OB.
∵OA·OB≤
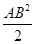 ,∴d·AB≤
,∴d·AB≤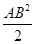 .
.∴AB≥2d=
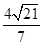 ,故当OA=OB时,弦AB的长度取得最小值
,故当OA=OB时,弦AB的长度取得最小值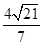 .
.
练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
 轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1 F2B2是一个面积为8的正方形.
轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1 F2B2是一个面积为8的正方形.
 中,已知
中,已知 分别是椭圆
分别是椭圆 的左、右焦点,椭圆
的左、右焦点,椭圆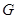 与抛物线
与抛物线 有一个公共的焦点,且过点
有一个公共的焦点,且过点 .
. 的方程;
的方程; 与椭圆
与椭圆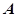 、
、 两点,若
两点,若 (
( 为坐标原点),试判断直线
为坐标原点),试判断直线 的位置关系,并证明你的结论.
的位置关系,并证明你的结论. 的两焦点,过点F2的直线交椭圆于A,B两点.在
的两焦点,过点F2的直线交椭圆于A,B两点.在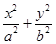 =1(a>b>0)的左、右顶点分别是A、B,左、右焦点分别是F1、F2.若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为________.
=1(a>b>0)的左、右顶点分别是A、B,左、右焦点分别是F1、F2.若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为________.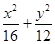 =1的左、右焦点分别为F1,F2,M是椭圆上一点,N是MF1的中点,若|ON|=1,则|MF1|等于( ).
=1的左、右焦点分别为F1,F2,M是椭圆上一点,N是MF1的中点,若|ON|=1,则|MF1|等于( ). 为椭圆
为椭圆 的两个焦点,过
的两个焦点,过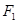 的直线交椭圆于
的直线交椭圆于 两点,
两点, ,则
,则 ( )
( )

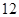

 的左、右焦点,点P是椭圆上的点,I是△F1PF2内切圆的圆心,直线PI交x轴于点M,则∣PI∣:∣IM∣的值为( )
的左、右焦点,点P是椭圆上的点,I是△F1PF2内切圆的圆心,直线PI交x轴于点M,则∣PI∣:∣IM∣的值为( )

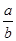

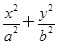 =1(a>b>0),它的一个顶点为M(0,1),离心率e=
=1(a>b>0),它的一个顶点为M(0,1),离心率e=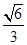 ,则椭圆的方程为( ).
,则椭圆的方程为( ). =1
=1 =1
=1 +y2=1
+y2=1 +y2=1
+y2=1