题目内容
已知椭圆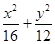 =1的左、右焦点分别为F1,F2,M是椭圆上一点,N是MF1的中点,若|ON|=1,则|MF1|等于( ).
=1的左、右焦点分别为F1,F2,M是椭圆上一点,N是MF1的中点,若|ON|=1,则|MF1|等于( ).
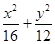 =1的左、右焦点分别为F1,F2,M是椭圆上一点,N是MF1的中点,若|ON|=1,则|MF1|等于( ).
=1的左、右焦点分别为F1,F2,M是椭圆上一点,N是MF1的中点,若|ON|=1,则|MF1|等于( ).| A.2 | B.4 | C.6 | D.5 |
C
由椭圆方程知a=4,∴|MF1|+|MF2|=8,
∴|MF1|=8-|MF2|=8-2|ON|=8-2=6.
∴|MF1|=8-|MF2|=8-2|ON|=8-2=6.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
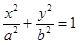 (a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,斜率为1的直线
(a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,斜率为1的直线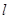 与椭圆C交于不同两点M,N.
与椭圆C交于不同两点M,N.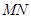 的长;
的长;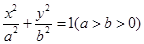 的离心率为
的离心率为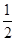 ,且经过点
,且经过点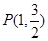 . 过它的两个焦点
. 过它的两个焦点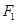 ,
,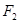 分别作直线
分别作直线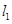 与
与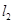 ,
,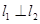 .
.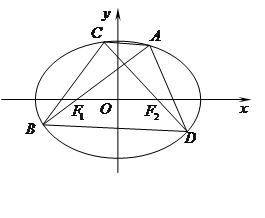
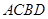 的面积
的面积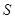 的取值范围.
的取值范围.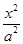 +
+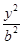 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=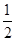 ,右焦点为F(c,0),方程ax2+2bx+c=0的两个实数根分别是x1和x2,则点P(x1,x2)到原点的距离为( )
,右焦点为F(c,0),方程ax2+2bx+c=0的两个实数根分别是x1和x2,则点P(x1,x2)到原点的距离为( )


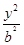 =1(0<b<1)的左、右焦点,过F1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.
=1(0<b<1)的左、右焦点,过F1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列. =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,右焦点到直线
,右焦点到直线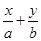 =1的距离d=
=1的距离d=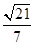 ,O为坐标原点.
,O为坐标原点. (
( >b>0)的离心率e=
>b>0)的离心率e=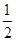 ,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D点,则tan∠BDC的值等于 ( )
,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D点,则tan∠BDC的值等于 ( ) 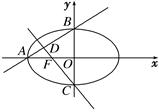
 B.
B. D.
D.
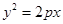 与椭圆
与椭圆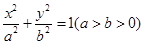 有相同的焦点
有相同的焦点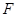 ,
,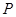 是两曲线的公共点,若
是两曲线的公共点,若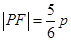 ,则此椭圆的离心率为 .
,则此椭圆的离心率为 .