题目内容
(本题满分12分)已知数列 为等差数列,且
为等差数列,且 ,数列
,数列 的前
的前 项和为
项和为 ,
, 且
且
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)若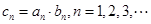 ,求数列
,求数列 的前
的前 项和
项和 .
.
 为等差数列,且
为等差数列,且 ,数列
,数列 的前
的前 项和为
项和为 ,
, 且
且
(Ⅰ)求数列
 ,
, 的通项公式;
的通项公式; (Ⅱ)若
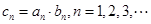 ,求数列
,求数列 的前
的前 项和
项和 .
.(Ⅰ)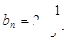 (Ⅱ)
(Ⅱ)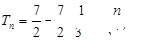
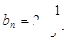 (Ⅱ)
(Ⅱ)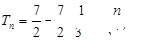
(Ⅰ)数列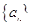 为等差数列,公差
为等差数列,公差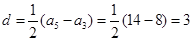 ,所以
,所以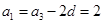 ,
,
故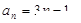 2分
2分
由已知得当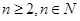 时,
时,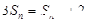 ,所以有
,所以有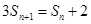
两式相减得: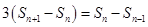 ,即
,即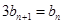 ,所以
,所以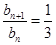
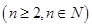 5分
5分
又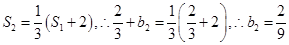 ,从而
,从而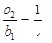 ,
,
所以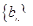 是以
是以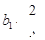 为首项,
为首项,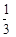 为公比的等比数列,于是
为公比的等比数列,于是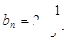 6分
6分
(Ⅱ)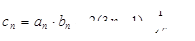
∴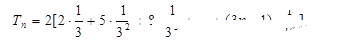 7分
7分
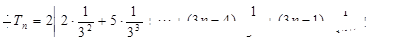 9分
9分
两式相减得 11分
11分
所以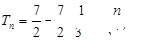 12分
12分
【考点定位】本题主要考查等差数列、等比数列的基础知识,考查“错位相减法”求和,意在考查考生的运算能力、逻辑思维能力以及转化与化归思想的运用.
 为等差数列,公差
为等差数列,公差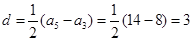 ,所以
,所以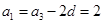 ,
,故
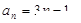 2分
2分由已知得当
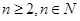 时,
时,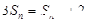 ,所以有
,所以有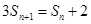
两式相减得:
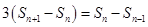 ,即
,即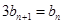 ,所以
,所以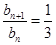
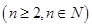 5分
5分又
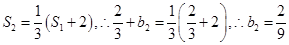 ,从而
,从而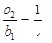 ,
,所以
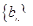 是以
是以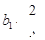 为首项,
为首项,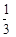 为公比的等比数列,于是
为公比的等比数列,于是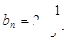 6分
6分(Ⅱ)
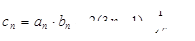
∴
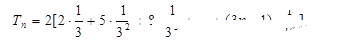 7分
7分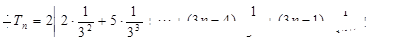 9分
9分两式相减得
 11分
11分所以
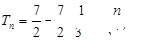 12分
12分【考点定位】本题主要考查等差数列、等比数列的基础知识,考查“错位相减法”求和,意在考查考生的运算能力、逻辑思维能力以及转化与化归思想的运用.

练习册系列答案
相关题目
 中各项均为正,有
中各项均为正,有 ,
,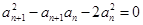 ,
, 中,
中, ,点
,点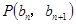 在直线
在直线 上.
上. 和
和 的值;(2)求数列
的值;(2)求数列 和
和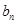 ;
; ,求数列
,求数列 的前n项和
的前n项和 .
.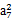 +2a11=0,数列{bn}是等比数列,且b7=a7,则b6b8=( )
+2a11=0,数列{bn}是等比数列,且b7=a7,则b6b8=( )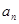 }是等差数列,
}是等差数列,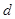 为其公差,
为其公差, 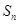 是其前
是其前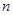 项和,若只有
项和,若只有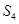 是{
是{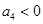 ③
③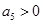 ④
④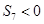 ⑤
⑤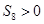
 的前
的前 项和为
项和为 ,公差
,公差 ,且
,且 .
. 是首项为1,公比为
是首项为1,公比为 的等比数列,求数列
的等比数列,求数列 的前n项和
的前n项和 .
. 中,
中, ,那么
,那么 .
.