题目内容
(本小题满分12分)
已知椭圆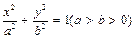 的左、右焦点分别为
的左、右焦点分别为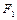 、
、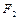 ,离心率
,离心率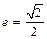 ,右准线方程为
,右准线方程为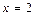 .
.
(I)求椭圆的标准方程;
(II)过点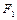 的直线
的直线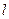 与该椭圆交于M、N两点,且
与该椭圆交于M、N两点,且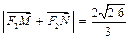 ,求直线
,求直线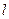 的方程.
的方程.
已知椭圆
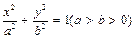 的左、右焦点分别为
的左、右焦点分别为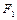 、
、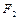 ,离心率
,离心率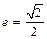 ,右准线方程为
,右准线方程为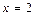 .
.(I)求椭圆的标准方程;
(II)过点
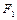 的直线
的直线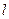 与该椭圆交于M、N两点,且
与该椭圆交于M、N两点,且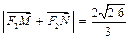 ,求直线
,求直线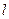 的方程.
的方程..解:
(Ⅰ)有条件有
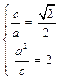 ,解得
,解得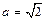 ,
,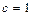 .
.∴
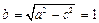
所以,所求椭圆的方程为
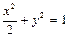 …………………………… 4分
…………………………… 4分(Ⅱ)由(Ⅰ)知
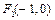 、
、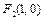 .
.若直线l的斜率不存在,则直线l的方程为
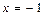 .
.将
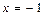 代入椭圆方程得:
代入椭圆方程得: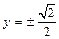 .
.不妨设
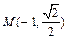 、
、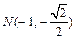 ,
,∴
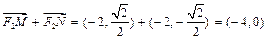
∴
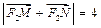 ,与题设矛盾.
,与题设矛盾.所以,直线l的斜率存在.设直线l的斜率为k,则直线的方程为
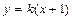 .
.设
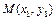 、
、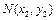 ,联立方程组
,联立方程组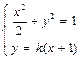 ,消y得:
,消y得: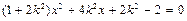
由根与系数的关系知
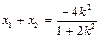 ,从而
,从而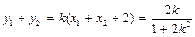 .
.又∵
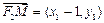 ,
,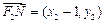
∴
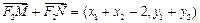
∴
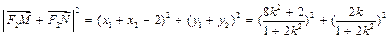
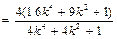
∴
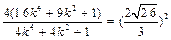 .
.化简得:
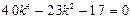
解得:
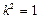 或
或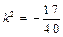
∴
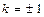
略

练习册系列答案
相关题目
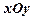 中,椭圆
中,椭圆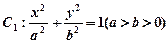 的左、右焦点分别为
的左、右焦点分别为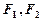 . 其中
. 其中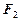 也是抛物线
也是抛物线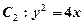 的焦点,点
的焦点,点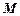 为
为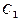 与
与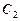 在第一象限的交点,且
在第一象限的交点,且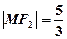
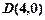 的直线
的直线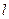 与
与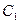 交于不同的两点
交于不同的两点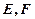 .
.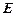 在
在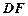 之间,试求
之间,试求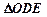 与
与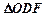 面积之比的取值范围.(O为坐标原点)
面积之比的取值范围.(O为坐标原点)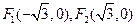 ,且椭圆短轴的两个端点与
,且椭圆短轴的两个端点与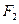 构成正三角形.
构成正三角形. 与椭圆交于不同两点P、Q,若在
与椭圆交于不同两点P、Q,若在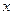 轴上存在定点E(
轴上存在定点E(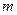 ,0),使
,0),使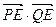 恒为定值,求
恒为定值,求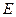 :
: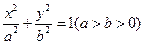 的离心率为
的离心率为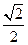 ,且过点
,且过点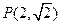 ,设椭圆的右准线
,设椭圆的右准线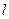 与
与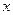 轴的交点为
轴的交点为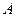 ,椭圆的上顶点为
,椭圆的上顶点为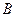 ,直线
,直线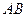 被以原点为圆心的圆
被以原点为圆心的圆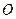 所截得的弦长为
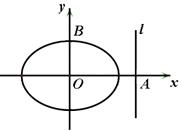
所截得的弦长为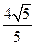 .
.
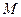 是准线
是准线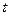 的点,求证:存在一个异于
的点,求证:存在一个异于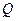 ,对于圆
,对于圆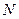 ,有
,有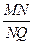 为定值;且当
为定值;且当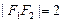
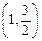 在椭圆C上.
在椭圆C上.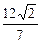 ,求以F2为圆
,求以F2为圆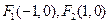 的椭圆经过点
的椭圆经过点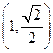 , 直线
, 直线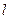 过点
过点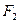 与椭圆交于
与椭圆交于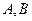 两点, 其中
两点, 其中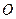 为坐标原点.
为坐标原点.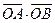 的范围;
的范围; 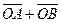 与向量
与向量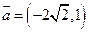 共线, 求
共线, 求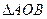 的外接圆方程.
的外接圆方程. 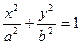
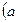 >
>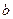 >
>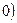 与直线
与直线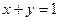 交于
交于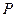 、
、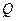 两点,且
两点,且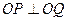 ,其
,其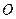 为坐标原点。
为坐标原点。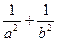 的值;
的值;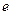 满足
满足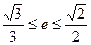 ,求椭圆长轴的取值范围。
,求椭圆长轴的取值范围。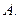
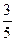
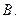
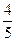
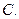
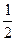
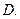
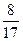
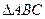 的顶点B、C在椭圆
的顶点B、C在椭圆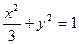 上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC 边上,则
上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC 边上,则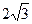 B. 6 C.
B. 6 C. 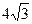 D. 12
D. 12