题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)若![]() 在
在![]() 上成立,求
上成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(2)
;(2)![]() .
.
【解析】
(1)![]() ,利用
,利用![]() ,解得
,解得![]() ,即可得出单调区间.
,即可得出单调区间.
(2)法一:由![]() 得
得![]() ,即
,即![]() .令
.令![]() ,利用导数研究其单调性即可得出.
,利用导数研究其单调性即可得出.
法二:由![]() 得
得![]() ,即
,即![]() ,令
,令![]() ,利用导数研究其单调性即可得出.
,利用导数研究其单调性即可得出.
解:(1)![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
故![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)法一:由![]() 得
得![]() ,即
,即![]() ,
,
令![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
又![]() ,
,![]() ,
,
所以![]() 有唯一的零点
有唯一的零点![]() ,
,
且当![]() 时,
时,![]() ,即
,即![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,即
,即![]() ,
,![]() 单调递增,
单调递增,
所以![]() ,
,
又因为![]() 所以
所以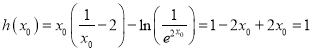 ,
,
所以![]() ,
,![]() 的取值范围是
的取值范围是![]() .
.
法二:由![]() 得
得![]() ,
,
即![]() ,
,
令![]() ,因为
,因为![]() ,
,![]() ,
,
所以![]() 存在零点
存在零点![]() ;
;
令![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
所以![]() ,
,
所以![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() .
.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(第![]() 周)和市场占有率(
周)和市场占有率(![]() )的几组相关数据如下表:
)的几组相关数据如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据上述线性回归方程,预测在第几周,该款旗舰机型市场占有率将首次超过![]() (最后结果精确到整数).
(最后结果精确到整数).
参考公式: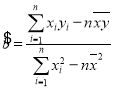 ,
,![]() .
.
【题目】在某区“创文明城区”(简称“创城”)活动中,教委对本区![]() 四所高中学校按各校人数分层抽样,随机抽查了100人,将调查情况进行整理后制成下表:
四所高中学校按各校人数分层抽样,随机抽查了100人,将调查情况进行整理后制成下表:
学校 |
|
|
|
|
抽查人数 | 50 | 15 | 10 | 25 |
“创城”活动中参与的人数 | 40 | 10 | 9 | 15 |
(注:参与率是指:一所学校“创城”活动中参与的人数与被抽查人数的比值)假设每名高中学生是否参与”创城”活动是相互独立的.
(1)若该区共2000名高中学生,估计![]() 学校参与“创城”活动的人数;
学校参与“创城”活动的人数;
(2)在随机抽查的100名高中学生中,随机抽取1名学生,求恰好该生没有参与“创城”活动的概率;
(3)在上表中从![]() 两校没有参与“创城”活动的同学中随机抽取2人,求恰好
两校没有参与“创城”活动的同学中随机抽取2人,求恰好![]() 两校各有1人没有参与“创城”活动的概率是多少?
两校各有1人没有参与“创城”活动的概率是多少?