题目内容
【题目】已知函数f（x）= 
，若关于x的方程f2（x）﹣bf（x）+c=0（b，c∈R）有8个不同的实数根，则b+c的取值范围为（ ）
A.（﹣∞，3）
B.（0，3]
C.[0，3]
D.（0，3）
【答案】D
【解析】解：根据题意作出f（x）的简图：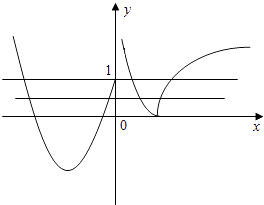 
由图象可得当f（x）∈（0，1]时，有四个不同的x与f（x）对应．再结合题中“方程f2（x）﹣bf（x）+c=0有8个不同实数解”，
可以分解为形如关于k的方程k2﹣bk+c=0有两个不同的实数根K1、K2 ， 且K1和K2均为大于0且小于等于1的实数．
列式如下：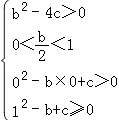 
，化简得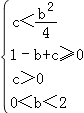 
，
此不等式组表示的区域如图：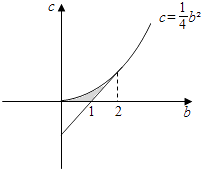
令z=b+c，则z=b+c在（2，1）处z=3，在（0，0）处z=0，
所以b+c的取值范围为（0，3），
故选：D．
练习册系列答案
相关题目
