题目内容
【题目】已知圆锥曲线 E: ![]() .
.
(I)求曲线 E的离心率及标准方程;
(II)设 M(x0 , y0)是曲线 E上的任意一点,过原点作⊙M:(x﹣x0)2+(y﹣y0)2=8的两条切线,分别交曲线 E于点 P、Q.
①若直线OP,OQ的斜率存在分别为k1 , k2 , 求证:k1k2=﹣ ![]() ;
;
②试问OP2+OQ2是否为定值.若是求出这个定值,若不是请说明理由.
【答案】解:(I)由椭圆定义可知,曲线E是以 ![]() 和
和 ![]() 为焦点,长轴长为
为焦点,长轴长为 ![]() 的椭圆,
的椭圆,
设椭圆的半长轴长、半短轴长、半焦距分别为a、b、c.
∴ ![]() ,
, ![]() ,则
,则 ![]() ,
,
∴椭圆的离心率 ![]() ,E的标准方程为
,E的标准方程为 ![]() .
.
(II)①证明:若过原点与⊙M相切的直线斜率存在设为k,
则切线方程为y=kx,∴ ![]() ,
,
整理得 ![]() .
.
由题设可知k1 , k2是以上关于k的一元二次方程的两个实根,
∴ 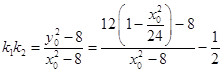 ,即
,即 ![]() .
.
②设 P(x1 , y1),Q(x2 , y2).
当直线 O P,OQ的斜率存在时,
由①易得 ![]() ,
, ![]() ,
,
而 ![]() =
= ![]() =
= ![]() =
= 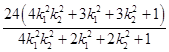 =
= 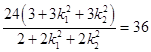
当直线 O P或 OQ的斜率不存在时,圆 M与y轴相切,且圆 M也与x轴相切 P,Q是椭圆 E的两个顶点,∴O P2+OQ2=a2+b2=36.
综上所述:O P2+OQ2为定值36.
【解析】(I)由椭圆定义可知,曲线E是以 ![]() 和
和 ![]() 为焦点,长轴长为
为焦点,长轴长为 ![]() 的椭圆,即可得出.(II)①若过原点与⊙M相切的直线斜率存在设为k,则切线方程为y=kx,可得
的椭圆,即可得出.(II)①若过原点与⊙M相切的直线斜率存在设为k,则切线方程为y=kx,可得 ![]() ,整理得
,整理得 ![]() .由题设可知k1 , k2是以上关于k的一元二次方程的两个实根,利用根与系数的关系即可得出.②设 P(x1 , y1),Q(x2 , y2).当直线 O P,OQ的斜率存在时,由①易得
.由题设可知k1 , k2是以上关于k的一元二次方程的两个实根,利用根与系数的关系即可得出.②设 P(x1 , y1),Q(x2 , y2).当直线 O P,OQ的斜率存在时,由①易得 ![]() ,
, ![]() ,利用两点之间的距离、根与系数的关系即可得出.当直线 O P,OQ的斜率不存在时直接验证即可得出.
,利用两点之间的距离、根与系数的关系即可得出.当直线 O P,OQ的斜率不存在时直接验证即可得出.

 金博士一点全通系列答案
金博士一点全通系列答案【题目】某大学城校区与本部校区之间的驾车单程所需时间为![]() ,
,![]() 只与道路畅通状况有关,对其容量为500的样本进行统计,结果如下:
只与道路畅通状况有关,对其容量为500的样本进行统计,结果如下:
| 25 | 30 | 35 | 40 |
频数(次) | 100 | 150 | 200 | 50 |
以这500次驾车单程所需时间的频率代替某人1次驾车单程所需时间的概率.
(1)求![]() 的分布列与
的分布列与![]() ;
;
(2)某天有3位教师独自驾车从大学城校区返回本部校区,记![]() 表示这3位教师中驾车所用时间少于
表示这3位教师中驾车所用时间少于![]() 的人数,求
的人数,求![]() 的分布列与
的分布列与![]() ;
;
(3)下周某天张老师将驾车从大学城校区出发,前往本部校区做一个50分钟的讲座,结束后立即返回大学城校区,求张老师从离开大学城校区到返回大学城校区共用时间不超过120分钟的概率.