题目内容
【题目】已知某企业生产某种产品的年固定成本为![]() 万元,且每生产
万元,且每生产![]() 吨该产品需另投入
吨该产品需另投入![]() 万元,现假设该企业在一年内共生产该产品
万元,现假设该企业在一年内共生产该产品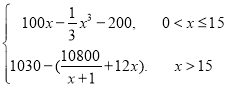 吨并全部销售完.每吨的销售收入为
吨并全部销售完.每吨的销售收入为![]() 万元,且
万元,且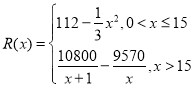
(1)求该企业年总利润![]() (万元)关于年产量
(万元)关于年产量![]() (吨)的函数关系式:
(吨)的函数关系式:
(2)当年产量为多少吨时,该企业在这一产品的生产中所获年总利润最大?
【答案】(1)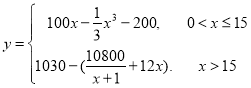 (2)
(2)![]() 吨
吨
【解析】
(1)根据题意分![]() 和
和![]() 两种情况得到
两种情况得到![]() 与
与![]() 的分段函数关系式;
的分段函数关系式;
(2)当![]() 时,利用导数研究函数的最大值,当
时,利用导数研究函数的最大值,当![]() 时,利用基本不等式来求
时,利用基本不等式来求![]() 的最大值,在进行比较,从而可得结果.
的最大值,在进行比较,从而可得结果.
(1)由题意![]()
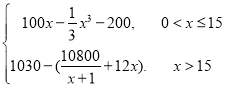
(2)当![]() 时,
时,![]() ,
,![]()
![]() 时,
时,![]() 时
时![]() ,∴函数在
,∴函数在![]() 递增,在
递增,在![]() 递减,∴当且仅当
递减,∴当且仅当![]() 时,
时,![]() 有最大值
有最大值![]() ;
;
当![]() 时,
时,![]()
![]()
![]() ,
,
![]() ,
,
当且仅当![]() ,即
,即![]() 时,
时,![]() 取最大值322.
取最大值322.
![]() ,∴当且仅当
,∴当且仅当![]() 时,
时,![]() 有最大值
有最大值![]() .
.
故当年产量为![]() 吨时,该化工厂在这一产品的生产中所获年利润最大,最大利润为
吨时,该化工厂在这一产品的生产中所获年利润最大,最大利润为![]() 万元.
万元.

【题目】某校高三课外兴趣小组为了了解高三同学高考结束后是否打算观看2018年足球世界杯比赛的情况,从全校高三年级1500名男生、1000名女生中按分层抽样的方式抽取125名学生进行问卷调查,情况如下表:
打算观看 | 不打算观看 | |
女生 | 20 | b |
男生 | c | 25 |
(1)求出表中数据b,c;
(2)判断是否有99%的把握认为观看2018年足球世界杯比赛与性别有关;
(3)在打算观看2018年足球世界杯比赛的同学中有5名男生、2名女生来自高三(5)班,从中推选5人接受校园电视台采访,请根据上述方法,求被推选出的5人中恰有四名男生、一名女生的概率.
附:
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
![]()
![]()
【题目】詹姆斯·哈登(James Harden)是美国NBA当红球星,自2012年10月加盟休斯顿火箭队以来,逐渐成长为球队的领袖.2017-18赛季哈登当选常规赛MVP(最有价值球员).
年份 | 2012-13 | 2013-14 | 2014-15 | 2015-16 | 2016-17 | 2017-18 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
常规赛场均得分y | 25.9 | 25.4 | 27.4 | 29.0 | 29.1 | 30.4 |
(Ⅰ)根据表中数据,求y关于t的线性回归方程![]() (
(![]() ,
,![]()
![]() *);
*);
(Ⅱ)根据线性回归方程预测哈登在2019-20赛季常规赛场均得分.
(附)对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:![]() ,
,![]()
(参考数据![]() ,计算结果保留小数点后一位)
,计算结果保留小数点后一位)