题目内容
【题目】过双曲线
的左焦点
作圆
的切线交双曲线的右支于点
，且切点为
，已知
为坐标原点，
为线段
的中点（点在切点的右侧），若
的周长为
，则双曲线的渐近线的方程为( )
A. 
B. 
C. 
D. 
【答案】B
【解析】
先从双曲线方程得：a，b．连OT，则OT⊥F1T，在直角三角形OTF1中，|F1T|＝b．连PF2，M为线段F1P的中点，O为坐标原点得出|MO|﹣|MT|
PF2﹣（ 
MF1﹣F1T）（PF2﹣MF1）﹣b最后结合周长与勾股定理可得结果.
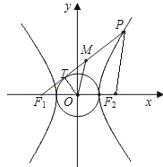
解：连OT，则OT⊥F1T，
在直角三角形OTF1中，|F1T|
b．
连PF2，M为线段F1P的中点，O为坐标原点
∴OMPF2，
∴|MO|﹣|MT|PF2﹣（ PF1﹣F1T）（PF2﹣PF1）+b
b﹣a．
又|MO|+|MT|+|TO|=
，即|MO|+|MT|=3a
故|MO|=
, |MT|=
,
由勾股定理可得：
，即
∴渐近线方程为：
故选：B
练习册系列答案
相关题目
