题目内容
6.已知函数$f(x)=2{sin^2}(\frac{π}{4}+x)+\sqrt{3}$cos2x.(1)求函数f(x)的最小正周期和对称轴方程;
(2)若关于x的方程f(x)-m=2在$x∈[0,\frac{π}{2}]$上有两个不同的解,求实数m的取值范围.
分析 (1)利用三角函数的倍角公式以及辅助角公式将函数进行化简即可求最小正周期和对称轴方程;
(2)求出函数f(x)在x∈[0,$\frac{π}{2}$]的取值情况,利用数形结合即可得到结论.
解答 解:(1)由$f(x)=2si{n}^{2}(\frac{π}{4}+x)+\sqrt{3}$=1-cos($\frac{π}{2}$+2x)+$\sqrt{3}$cos2x=1+sin2x+$\sqrt{3}$cos2x=1+2sin(2x+$\frac{π}{3}$),
∵ω=2,
∴函数f(x)的最小正周期为π,
由2x+$\frac{π}{3}$=$\frac{π}{2}$+kπ,k∈Z得:x=$\frac{π}{12}$+$\frac{1}{2}$kπ,k∈Z,
故函数f(x)的对称轴方程为:x=$\frac{π}{12}$+$\frac{1}{2}$kπ,k∈Z,
(2)由f(x)-m=2得f(x)=m+2,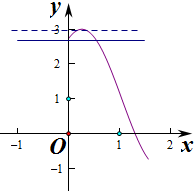
当x∈[0,$\frac{π}{2}$]时,2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{4π}{3}$],
由图象得f(0)=1+2sin$\frac{π}{3}$=1+$\sqrt{3}$,
函数f(x)的最大值为1+2=3,
∴要使方程f(x)-m=2在x∈[0,$\frac{π}{2}$]上有两个不同的解,
则f(x)=m+2在x∈[0,$\frac{π}{2}$]上有两个不同的解,
即函数f(x)和y=m+2在x∈[0,$\frac{π}{2}$]上有两个不同的交点,
即1+$\sqrt{3}$≤m+2<3,
即$\sqrt{3}$-1≤m<1.
点评 本题主要考查三角函数的图象和性质,利用辅助角公式将函数进行化简,利用数形结合是解决本题的关键.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案| A. | 100 | B. | $\frac{1}{100}$ | C. | 101 | D. | $\frac{1}{101}$ |

| A. | 55,10 | B. | 220,11 | C. | 110,10 | D. | 110,11 |
| A. | -110 | B. | -90 | C. | 90 | D. | 110 |
| A. | 2f(1)>f(2) | B. | 2f(1)<f(2) | ||
| C. | 2f(1)=f(2) | D. | 2f(1)与f(2)大小不确定 |