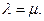题目内容
已知平面α∥β,直线l?α,点P∈l,平面α、β间的距离为5,则在β内到点P的距离为13且到直线l的距离为5
的点的轨迹是( )
| 2 |
| A.一个圆 | B.四个点 |
| C.两条直线 | D.双曲线的一支 |
如图所示:作PH⊥β,H为垂足,则PH=5.
过H 作直线m∥l,则m是l在平面β内的射影.
作HA⊥m,且HA=PH=5,
则由三垂线定理可得 PA⊥m,∴PA⊥l,故 PA=5
.
作AM∥m,且 AM=
,有勾股定理可得MP=13,故M在所求的轨迹上.又点M在面β内,
故满足条件的M共有4个,
故选 B.
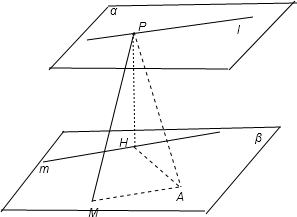
过H 作直线m∥l,则m是l在平面β内的射影.
作HA⊥m,且HA=PH=5,
则由三垂线定理可得 PA⊥m,∴PA⊥l,故 PA=5
| 2 |
作AM∥m,且 AM=
| 119 |
故满足条件的M共有4个,
故选 B.


练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
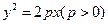 上一定点
上一定点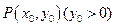 ,作两条直线分别交抛物线于
,作两条直线分别交抛物线于 ,(1)求该抛物线上纵坐标为
,(1)求该抛物线上纵坐标为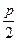 的点到其焦点
的点到其焦点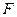 的距离;(2)当
的距离;(2)当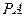 与
与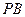 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求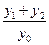 的值,并证明直线
的值,并证明直线 的斜率是非零常数。
的斜率是非零常数。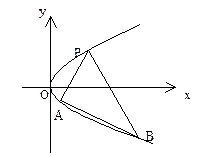
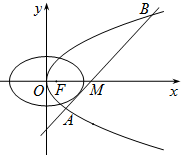
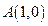 和到定直线
和到定直线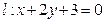 的距离相等的点的轨迹为( )
的距离相等的点的轨迹为( )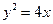 ,
,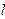 为其准线,过其对称轴上一点P
为其准线,过其对称轴上一点P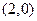 作直线
作直线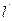 与抛物线交于A
与抛物线交于A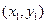 、B
、B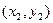 两点,连结OA、OB并延长AO、BO分别交
两点,连结OA、OB并延长AO、BO分别交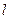 于点M、N。(1)求
于点M、N。(1)求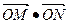 的值;
的值;
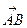 所成的比为
所成的比为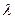 ,
,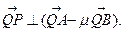 求证:
求证: