题目内容
如图,过抛物线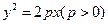 上一定点
上一定点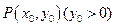 ,作两条直线分别交抛物线于
,作两条直线分别交抛物线于 ,(1)求该抛物线上纵坐标为
,(1)求该抛物线上纵坐标为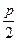 的点到其焦点
的点到其焦点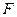 的距离;(2)当
的距离;(2)当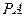 与
与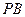 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求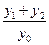 的值,并证明直线
的值,并证明直线 的斜率是非零常数。
的斜率是非零常数。
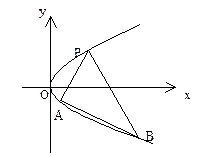
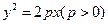 上一定点
上一定点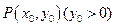 ,作两条直线分别交抛物线于
,作两条直线分别交抛物线于 ,(1)求该抛物线上纵坐标为
,(1)求该抛物线上纵坐标为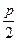 的点到其焦点
的点到其焦点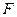 的距离;(2)当
的距离;(2)当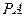 与
与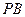 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求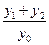 的值,并证明直线
的值,并证明直线 的斜率是非零常数。
的斜率是非零常数。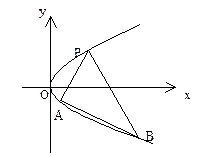
⑴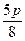 ⑵-2
⑵-2
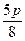 ⑵-2
⑵-222.(1)当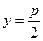 时,
时, ,又抛物线
,又抛物线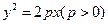 的准线方程为
的准线方程为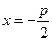 ,由抛物线的定义得:所求距离为
,由抛物线的定义得:所求距离为 。
。
(2)设直线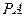 的斜率为
的斜率为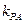 ,直线
,直线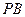 的斜率为
的斜率为 ,由
,由 ,两式相减得
,两式相减得 。故
。故 ,同理可得
,同理可得 ,由
,由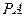 与
与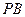 的斜率存在且倾斜角互补知:
的斜率存在且倾斜角互补知: ,即
,即 ,∴
,∴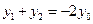 ,故
,故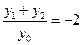 ,设直线
,设直线 的斜率为
的斜率为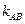 ,由
,由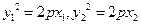 ,两式相减得
,两式相减得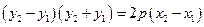 ,∴
,∴ ,将
,将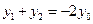 代入得
代入得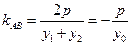 ,所以
,所以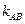 为非零常数。
为非零常数。
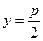 时,
时, ,又抛物线
,又抛物线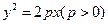 的准线方程为
的准线方程为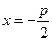 ,由抛物线的定义得:所求距离为
,由抛物线的定义得:所求距离为 。
。(2)设直线
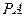 的斜率为
的斜率为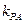 ,直线
,直线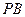 的斜率为
的斜率为 ,由
,由 ,两式相减得
,两式相减得 。故
。故 ,同理可得
,同理可得 ,由
,由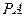 与
与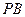 的斜率存在且倾斜角互补知:
的斜率存在且倾斜角互补知: ,即
,即 ,∴
,∴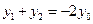 ,故
,故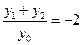 ,设直线
,设直线 的斜率为
的斜率为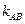 ,由
,由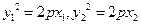 ,两式相减得
,两式相减得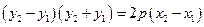 ,∴
,∴ ,将
,将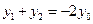 代入得
代入得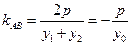 ,所以
,所以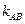 为非零常数。
为非零常数。
练习册系列答案
相关题目
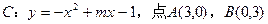
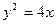
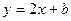
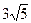
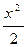 与过点M(0,-1)的直线l相交于A、B两点,O为坐标原点,若直线OA和OB斜率之和为1,求直线l的方程.
与过点M(0,-1)的直线l相交于A、B两点,O为坐标原点,若直线OA和OB斜率之和为1,求直线l的方程.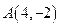 ,
,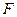 是抛物线
是抛物线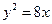 的焦点,点
的焦点,点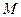 在抛物线上移动,当
在抛物线上移动,当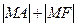 取最小值时,求点
取最小值时,求点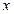 轴为对称轴,过焦点且垂直于对称轴的弦长为
轴为对称轴,过焦点且垂直于对称轴的弦长为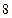 ,求抛物线的方程。
,求抛物线的方程。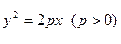 的轴和它的准线交于E点,经过焦点F的直线交抛物线于P、Q
的轴和它的准线交于E点,经过焦点F的直线交抛物线于P、Q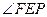 与
与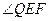 的大小关系为 ( )
的大小关系为 ( )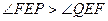
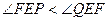
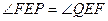
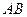 是抛物线
是抛物线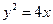 的焦点弦,且满足
的焦点弦,且满足 ,则直线
,则直线