题目内容
【题目】如图①,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() 为
为![]() 中点现将四边形
中点现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,得到如图②所示的多面体在图②中,
,得到如图②所示的多面体在图②中,
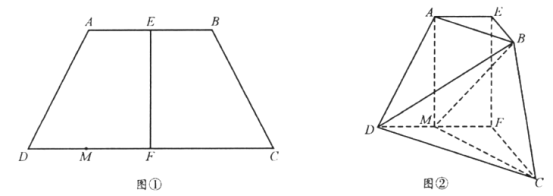
(1)证明:![]() ;
;
(2)求二面角![]() 的余弦值。
的余弦值。
【答案】(1)见证明;(2)![]()
【解析】
(1)由已知可得EF⊥AB,EF⊥CD,折叠后,EF⊥DF,EF⊥CF,利用线面垂直的判定得EF⊥平面DCF,从而得到EF⊥MC;(2)由平面![]() 平面
平面![]() ,得
,得![]() 平面
平面![]() ,得
,得![]() ,进一步得
,进一步得![]() ,
,![]() ,
,![]() 两两垂直.以
两两垂直.以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,求平面
,求平面![]() ,平面
,平面![]() 的法向量,求解即可
的法向量,求解即可
(1)由题意,可知在等腰梯形![]() 中,
中,![]() ,
,
∵![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,∴
的中点,∴![]() ,
,![]() .
.
∴折叠后,![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,∴
,∴![]() .
.
(2)∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ,
,![]() 两两垂直.
两两垂直.
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() .
.
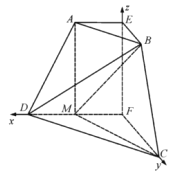
∵![]() ,∴
,∴![]() .
.
∴![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,![]() .
.
设平面![]() ,平面
,平面![]() 的法向量分别为
的法向量分别为
![]() ,
,![]() .
.
由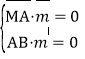 ,得
,得![]() .
.
取![]() ,则
,则![]() .
.
由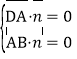 ,得
,得![]() .
.
取![]() ,则
,则![]() .
.
∵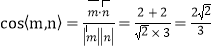 ,
,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
【题目】甲、乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们射击成绩的分布列如下表所示.
射手甲 | 射手乙 | ||||||
环数 |
|
|
| 环数 |
|
|
|
概率 |
|
|
| 概率 |
|
|
|
(1)若甲射手共有![]() 发子弹,一旦命中
发子弹,一旦命中![]() 环就停止射击,求他剩余
环就停止射击,求他剩余![]() 发子弹的概率;
发子弹的概率;
(2)若甲、乙两名射手各射击![]() 次,求
次,求![]() 次射击中恰有
次射击中恰有![]() 次命中
次命中![]() 环的概率;
环的概率;
(3)若甲、乙两名射手各射击![]() 次,记所得的环数之和为
次,记所得的环数之和为![]() ,求
,求![]() 的概率分布.
的概率分布.