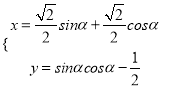题目内容
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]()
![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() ,
,![]() 的公共点为
的公共点为![]() .
.
(Ⅰ)求直线![]() 的斜率;
的斜率;
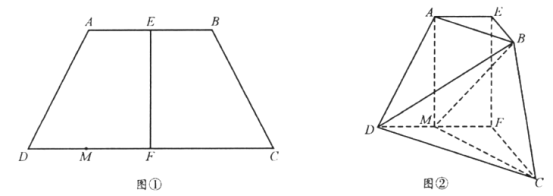
(Ⅱ)若点![]() 分别为曲线
分别为曲线![]() ,
,![]() 上的动点,当
上的动点,当![]() 取最大值时,求四边形
取最大值时,求四边形![]() 的面积.
的面积.
【答案】(Ⅰ)2;(Ⅱ)![]() .
.
【解析】
(Ⅰ)消去参数α得曲线C1的普通方程,将曲线C2化为直角坐标方程,两式作差得直线AB的方程,则直线AB的斜率可求;
(Ⅱ)由C1方程可知曲线是以C1(0,1)为圆心,半径为1的圆,由C2方程可知曲线是以C2(2,0)为圆心,半径为2的圆,又|CD|≤|CC1|+|C1C2|+|DC2|,可知当|CD|取最大值时,圆心C1,C2在直线AB上,进一步求出直线CD(即直线C1C2)的方程,再求出O到直线CD的距离,则四边形ACBD的面积可求.
(Ⅰ)消去参数α得曲线C1的普通方程C1:x2+y2﹣2y=0.…(1)
将曲线C2:ρ=4cosθ化为直角坐标方程得x2+y2﹣4x=0.…(2)
由(1)﹣(2)化简得y=2x,即为直线AB的方程,故直线AB的斜率为2;
(Ⅱ)由C1:x2+y2﹣2y=0知曲线C1是以C1(0,1)为圆心,半径为1的圆,
由C2:x2+y2﹣4x=0知曲线C2:是以C2(2,0)为圆心,半径为2的圆.
∵|CD|≤|CC1|+|C1C2|+|DC2|,
∴当|CD|取最大值时,圆心C1,C2在直线CD上,
∴直线CD(即直线C1C2)的方程为:2x+y=2.
∵O到直线CD的距离为![]() ,即|AB|=
,即|AB|=![]()
又此时|CD|=|C1C2|+1+2=3+![]() ,
,
∴四边形ACBD的面积![]() .
.

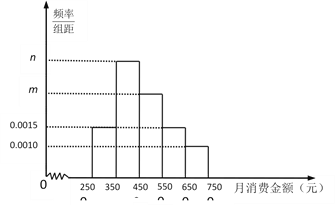
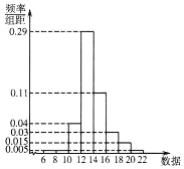
【题目】某机构为了解某地区中学生在校月消费情况,随机抽取了100名中学生进行调查.右图是根据调查的结果绘制的学生在校月消费金额的频率分布直方图.已知[350,450),[450,550),[550,650)三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群” .
(1)求m,n的值,并求这100名学生月消费金额的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)根据已知条件完成下面2×2列联表,并判断能否有90%的把握认为“高消费群”与性别有关?
高消费群 | 非高消费群 | 合计 | |
男 | |||
女 | 10 | 50 | |
合计 |
(参考公式:![]() ,其中
,其中![]() )
)
P( | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |