题目内容
2.根据下列给出的条件能得出△ABC为钝角三角形有( )①sinA+cosA=$\frac{1}{4}$; ②$\overrightarrow{AC}•\overrightarrow{CB}$=-$\frac{1}{3}$;
③sin2A+sin2B>sin2C; ④AB=3,AC=2,sinB=$\frac{1}{3}$.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 对四个条件分别分析判断三角形内角的大小.
解答 解:因为A,B,C是三角形的内角,
对于①由sinA+cosA=$\frac{1}{4}$,得到2sinAcosA=-$\frac{15}{16}$<0,所以cosA<0,所以A为钝角;
对于②,$\overrightarrow{AC}•\overrightarrow{CB}$=-$\frac{1}{3}$<0,根据商量下的定义得到向量$\overrightarrow{AC}$,$\overrightarrow{CB}$的夹角为钝角,而∠C为锐角;
对于③,sin2A+sin2B>sin2C,由正弦定理得到a2+b2>c2,再由余弦定理得到cosC>0,即C为锐角,但是A,B角不确定;
对于④,AB=3,AC=2,sinB=$\frac{1}{3}$,不能确定三角形ABC 的形状;
故选:D
点评 本题考查了三角形的形状判断,用到了三角函数式的等价变形、数量积公式、余弦定理等知识点;属于中档题.

练习册系列答案
相关题目
13.已知角α的终边与以坐标原点为圆心,以1为半径的圆交于点P(sin$\frac{2π}{3}$,cos$\frac{2π}{3}$),则角α的最小正值为( )
| A. | $\frac{11π}{6}$ | B. | $\frac{5π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
10.设a,b∈R,且a>b,则下列结论中正确的是( )
| A. | $\frac{a}{b}$>l | B. | $\frac{1}{a}$<$\frac{1}{b}$ | C. | |a|>|b| | D. | a3>b3 |
17.甲、乙两人约定在7:00~8:00之间在某处会面,且他们在这一时间段内任一时刻到达该处的可能性均相等,则他们中先到者等待的时间不超过15分钟的概率是( )
| A. | $\frac{9}{16}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{16}$ | D. | $\frac{5}{16}$ |
14.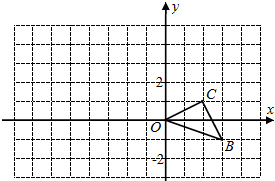 如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1).若以O为位似中心在y轴左侧将△OBC放大到两倍,得到△OB′C′,则△OB′C′的面积是( )
如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1).若以O为位似中心在y轴左侧将△OBC放大到两倍,得到△OB′C′,则△OB′C′的面积是( )
 如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1).若以O为位似中心在y轴左侧将△OBC放大到两倍,得到△OB′C′,则△OB′C′的面积是( )
如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1).若以O为位似中心在y轴左侧将△OBC放大到两倍,得到△OB′C′,则△OB′C′的面积是( )| A. | 20 | B. | 10 | C. | 5 | D. | $\frac{5}{2}$ |
11.等差数列的前三项依次为a-1,a+1,2a+3,那么这个等差数列的通项公式为( )
| A. | an=2n-4 | B. | an=2n-3 | C. | an=2n-1 | D. | an=2n+1 |