题目内容
10.已知函数f(x)=sin(ωx+$\frac{π}{6}$)(ω>0)的最小正周期为π,则该函数的图象( )| A. | 关于直线x=$\frac{π}{6}$对称 | B. | 关于直线x=$\frac{π}{4}$对称. | ||
| C. | 关于点($\frac{π}{4}$,0)对称 | D. | 关于点($\frac{π}{6}$,0)对称 |
分析 由条件利用正弦函数的图象的周期性求得ω的值,可得函数的解析式,再利用正弦函数的图象的对称性求出它的对称轴方程,从而得出结论.
解答 解:由于函数f(x)=sin(ωx+$\frac{π}{6}$)(ω>0)的最小正周期为$\frac{2π}{ω}$=π,可得ω=2,
函数f(x)=sin(2x+$\frac{π}{6}$).
令2x+$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,求得x=$\frac{kπ}{2}$+$\frac{π}{6}$,故函数的图象的对称轴方程为 x=$\frac{kπ}{2}$+$\frac{π}{6}$,k∈Z.
令2x+$\frac{π}{6}$=kπ,k∈Z,求得x=$\frac{kπ}{2}$-$\frac{π}{12}$,故函数的图象的对称轴中心为 x=$\frac{kπ}{2}$-$\frac{π}{12}$,k∈Z,
故选:A.
点评 本题主要考查正弦函数的图象的周期性和对称性,属于基础题.

练习册系列答案
相关题目
20.设函数$f(x)=\left\{\begin{array}{l}2{x^2}-x,x≤0\\-{x^2}+2x,x>0\end{array}\right.$,且关于x的方程f(x)=m,(m∈R)恰有3个不同的实数根x1,x2,x3,则x1x2x3的取值范围是( )
| A. | (-1,0) | B. | $(-\frac{1}{2},+∞)$ | C. | (0,1) | D. | $(-\frac{1}{2},0)$ |
15.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+3x(x≥0)}\\{g(x)(x<0)}\end{array}\right.$为奇函数,则f(g(-1))=( )
| A. | -28 | B. | -8 | C. | -4 | D. | 4 |
19.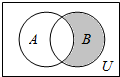 设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )
设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )
 设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )
设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )| A. | {3} | B. | {-2} | C. | {3,-2} | D. | {∅} |
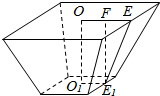 已知正四棱台高是12cm,两底面边长之差为10cm,全面积为512cm2.
已知正四棱台高是12cm,两底面边长之差为10cm,全面积为512cm2.