题目内容
20．设函数$f（x）=\left\{\begin{array}{l}2{x^2}-x，x≤0\\-{x^2}+2x，x＞0\end{array}\right.$，且关于x的方程f（x）=m，（m∈R）恰有3个不同的实数根x1，x2，x3，则x1x2x3的取值范围是（ ）| A． | （-1，0） | B． | $（-\frac{1}{2}，+∞）$ | C． | （0，1） | D． | $（-\frac{1}{2}，0）$ |
分析 画出函数f（x）的图象，不妨设x1＜x2＜x3，则-$\frac{1}{2}$＜x1＜0＜x2＜1＜x3＜2，由x2+x3=2，可得0＜x2x3＜1，由不等式的性质，即可得到所求范围．
解答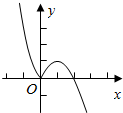 
解：画出函数$f（x）=\left\{\begin{array}{l}2{x^2}-x，x≤0\\-{x^2}+2x，x＞0\end{array}\right.$的图象，
依题意得关于x的方程f（x）=m，（m∈R）恰有三个互不相同的
实数根x1，x2，x3，不妨设x1＜x2＜x3，则
-$\frac{1}{2}$＜x1＜0＜x2＜1＜x3＜2，
又x2，x3关于x=1对称，则x2+x3=2，x2x3=-（x2-1）2+1，
∴0＜x2x3＜1，
∴-$\frac{1}{2}$＜x1x2x3＜0．
故选D．
点评 本题考查函数和方程的转化思想的运用，考查二次函数的对称性，以及数形结合的思想方法，运用不等式的性质，属于中档题．
练习册系列答案
相关题目
8．有下列关系：（1）人的年龄与他（她）体内脂肪含量之间的关系；（2）曲线上的点与该点的坐标之间的关系；（3）红橙的产量与气候之间的关系；（4）学生与他（她）的学号之间的关系．其中有相关关系的是（ ）
| A． | （1）、（2） | B． | （1）、（3） | C． | （1）、（4） | D． | （3）、（4） |
10．已知函数f（x）=sin（ωx+$\frac{π}{6}$）（ω＞0）的最小正周期为π，则该函数的图象（ ）
| A． | 关于直线x=$\frac{π}{6}$对称 | B． | 关于直线x=$\frac{π}{4}$对称． | ||
| C． | 关于点（$\frac{π}{4}$，0）对称 | D． | 关于点（$\frac{π}{6}$，0）对称 |