题目内容
20．
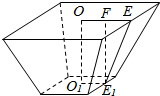已知正四棱台高是12cm，两底面边长之差为10cm，全面积为512cm2． （1）求上、下底面的边长．
（2）作出其三视图（单位长度为0.5厘米）．
分析 （1）设OE=xcm，则上底面边长为2xcm，下底面边长为（2x-10）cm，故O1E1=（x-5）cm，结合棱台的全面积为512cm2，解方程可得棱台的上、下底面的边长．
（2）由已知中的直观图可得棱锥的三视图．
解答 解：（1）设OE=xcm，则上底面边长为2xcm，下底面边长为（2x-10）cm，故O1E1=（x-5）cm，
则FE=5cm，
又∵正四棱台高是12cm，
∴EE1=13cm，
故正四棱台的全面积S=$（2x）^{2}+（2x-10）^{2}+4×\frac{1}{2}（2x+2x-10）×13$=8（x2-8x-20）=512cm2．
解得：x=14cm，
故正四棱台上底面边长为28cm，下底面边长为18cm，
（2）正四棱台的三视图如下图所示：
点评 本题考查的知识点是棱台的表面积，空间几何体的三视图，难度中档．
练习册系列答案
相关题目
10．已知函数f（x）=sin（ωx+$\frac{π}{6}$）（ω＞0）的最小正周期为π，则该函数的图象（ ）
| A． | 关于直线x=$\frac{π}{6}$对称 | B． | 关于直线x=$\frac{π}{4}$对称． | ||
| C． | 关于点（$\frac{π}{4}$，0）对称 | D． | 关于点（$\frac{π}{6}$，0）对称 |
如图是某几何体的正视图和俯视图，试分析此几何体的结构特征，并画出其侧视图．
5．若直线y=x+b与曲线x2-4x+y2-6y+9=0（y≤3）有公共点，则b的取值范围是（ ）
| A． | [-1，1+2$\sqrt{2}$] | B． | [1-2$\sqrt{2}$，1+2$\sqrt{2}$] | C． | [1-2$\sqrt{2}$，3] | D． | [1-$\sqrt{2}$，3] |