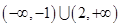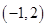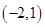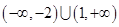题目内容
已知函数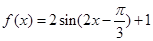 ,
,
(Ⅰ)求函数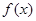 的单调递减区间;
的单调递减区间;
(Ⅱ)令函数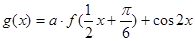 (
(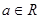 ),求函数
),求函数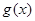 的最大值的表达式
的最大值的表达式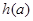 ;
;
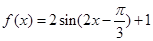 ,
, (Ⅰ)求函数
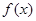 的单调递减区间;
的单调递减区间;(Ⅱ)令函数
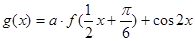 (
(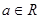 ),求函数
),求函数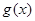 的最大值的表达式
的最大值的表达式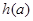 ;
;(Ⅰ)
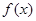 的单调递减区间为:
的单调递减区间为: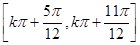
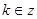
(Ⅱ)
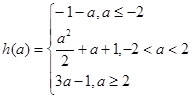
第一问中利用令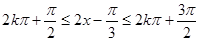 ,
,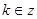 ,
,
∴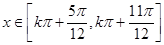 ,
,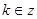
第二问中,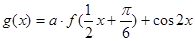 =
=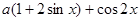
=
=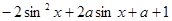 令
令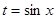 ,
,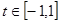 ,则
,则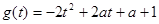 借助于二次函数分类讨论得到最值。
借助于二次函数分类讨论得到最值。
(Ⅰ)解:令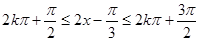 ,
,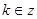 ,
,
∴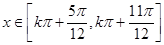 ,
,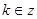
∴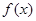 的单调递减区间为:
的单调递减区间为: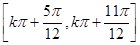
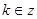 …………………4分
…………………4分
(Ⅱ)解: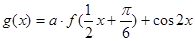 =
=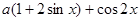
=
=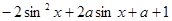
令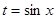 ,
,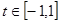 ,则
,则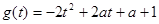 ……………………4分
……………………4分
对称轴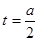
① 当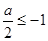 即
即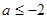 时,
时,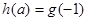 =
=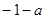 ……………1分
……………1分
② 当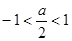 即
即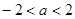 时,
时, =
=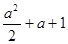 ……………1分
……………1分
③ 当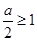 即
即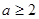 时,
时,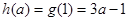 ……………1分
……………1分
综上: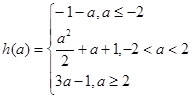
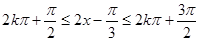 ,
,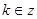 ,
,∴
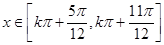 ,
,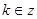
第二问中,
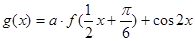 =
=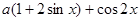
=

=
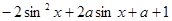 令
令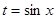 ,
,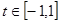 ,则
,则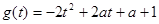 借助于二次函数分类讨论得到最值。
借助于二次函数分类讨论得到最值。(Ⅰ)解:令
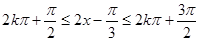 ,
,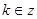 ,
,∴
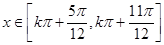 ,
,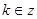
∴
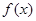 的单调递减区间为:
的单调递减区间为: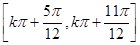
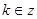 …………………4分
…………………4分(Ⅱ)解:
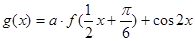 =
=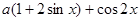
=

=
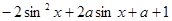
令
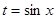 ,
,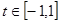 ,则
,则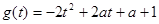 ……………………4分
……………………4分对称轴
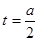
① 当
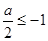 即
即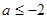 时,
时,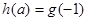 =
=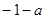 ……………1分
……………1分② 当
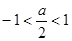 即
即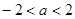 时,
时, =
=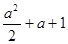 ……………1分
……………1分③ 当
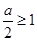 即
即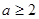 时,
时,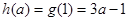 ……………1分
……………1分综上:
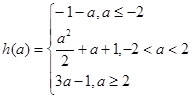

练习册系列答案
相关题目
 R,函数
R,函数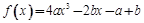 .
.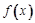 的最大值为|2a-b|﹢a;
的最大值为|2a-b|﹢a; 函数
函数
 的单调区间;
的单调区间; 的取值范围.
的取值范围.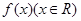 满足:
满足: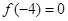 ,且在区间
,且在区间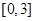 与
与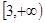 上分别递减和递增,则不等式
上分别递减和递增,则不等式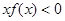 的解集为_____.
的解集为_____.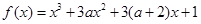 有极大值和极小值,则
有极大值和极小值,则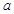 的取值范围是( )
的取值范围是( )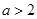 或
或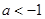
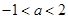
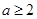 或
或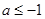
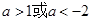
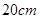 的铁丝剪成两段,并分别折成正方形,则这两个正方形的面积的和的最小值为( )
的铁丝剪成两段,并分别折成正方形,则这两个正方形的面积的和的最小值为( )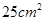
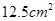
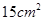

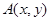 在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周,已知时间t=0时,点A(
在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周,已知时间t=0时,点A(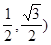 ,则0≤t≤12时,动点A的横坐标x关于t(单位:秒)的函数单调递减区间是( )
,则0≤t≤12时,动点A的横坐标x关于t(单位:秒)的函数单调递减区间是( )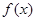 满足
满足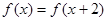 ,当
,当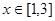 时,
时,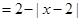 则
则 
 若
若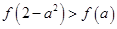 ,则实数
,则实数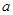 的取值范围是( )
的取值范围是( )