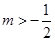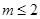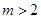题目内容
设 函数
函数
(I)求 的单调区间;
的单调区间;
(II)若函数 无零点,求实数
无零点,求实数 的取值范围.
的取值范围.
 函数
函数
(I)求
 的单调区间;
的单调区间;(II)若函数
 无零点,求实数
无零点,求实数 的取值范围.
的取值范围.(I)当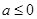 时,
时,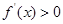 ,
, 单调递增;当
单调递增;当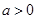 时,若
时,若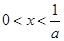 ,
,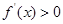 ,
, 单调递增;若
单调递增;若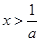 ,
,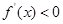 ,
, 单调递减;
单调递减;
(Ⅱ)实数 的取值范围是
的取值范围是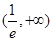
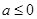 时,
时,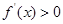 ,
, 单调递增;当
单调递增;当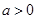 时,若
时,若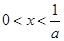 ,
,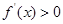 ,
, 单调递增;若
单调递增;若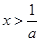 ,
,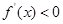 ,
, 单调递减;
单调递减;(Ⅱ)实数
 的取值范围是
的取值范围是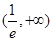
本试题主要是考查了导数在研究函数中的运用,求解函数 单调区间和函数的零点的概念的综合运用。
(1)先求解定义域然后求解导数,分析导数的符号,得到单调区间,注意对于参数a的分类讨论。
(2)根据第一问的结论可知当a在不同范围的时候,可以判定函数单调性,进而确定是否有零点的问题。解:因为
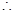 函数
函数 的定义域为
的定义域为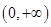 ,
,
且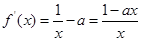 ,
,
(I)当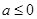 时,
时,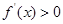 ,
, 单调递增;…………3分
单调递增;…………3分
当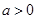 时,若
时,若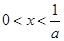 ,
,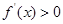 ,
, 单调递增;
单调递增;
若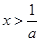 ,
,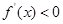 ,
, 单调递减;…………………………6分
单调递减;…………………………6分
(Ⅱ)①由(I)知当 时,
时, 在
在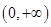 上单调递增
上单调递增
又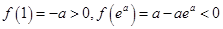
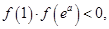 函数
函数 在区间
在区间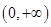 上有唯一零点…………………………8分
上有唯一零点…………………………8分
②当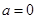 时,
时,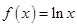 有唯一零点
有唯一零点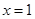 …………………………9分
…………………………9分
③当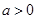 时,
时, 在
在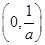 上是增函数;在
上是增函数;在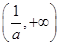 上是减函数;
上是减函数;
故在区间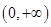 上,
上, 有极大值为
有极大值为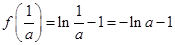 …………………11分
…………………11分
由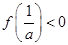 ,即
,即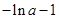 ,解得:
,解得: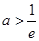 ……………………………13分
……………………………13分
故所求实数 的取值范围是
的取值范围是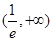
(1)先求解定义域然后求解导数,分析导数的符号,得到单调区间,注意对于参数a的分类讨论。
(2)根据第一问的结论可知当a在不同范围的时候,可以判定函数单调性,进而确定是否有零点的问题。解:因为

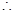 函数
函数 的定义域为
的定义域为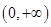 ,
,且
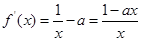 ,
,(I)当
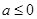 时,
时,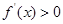 ,
, 单调递增;…………3分
单调递增;…………3分当
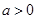 时,若
时,若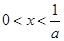 ,
,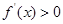 ,
, 单调递增;
单调递增;若
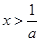 ,
,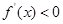 ,
, 单调递减;…………………………6分
单调递减;…………………………6分(Ⅱ)①由(I)知当
 时,
时, 在
在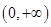 上单调递增
上单调递增又
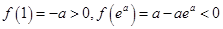
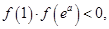 函数
函数 在区间
在区间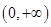 上有唯一零点…………………………8分
上有唯一零点…………………………8分②当
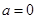 时,
时,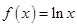 有唯一零点
有唯一零点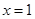 …………………………9分
…………………………9分③当
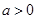 时,
时, 在
在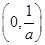 上是增函数;在
上是增函数;在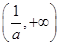 上是减函数;
上是减函数;故在区间
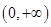 上,
上, 有极大值为
有极大值为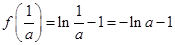 …………………11分
…………………11分由
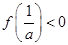 ,即
,即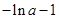 ,解得:
,解得: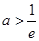 ……………………………13分
……………………………13分故所求实数
 的取值范围是
的取值范围是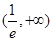

练习册系列答案
相关题目
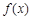 对于任意
对于任意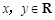 ,总有
,总有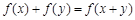 ,且x > 0时,
,且x > 0时,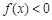 ,
,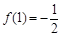 .
.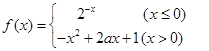
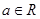 ,则下列结论正确的是( )
,则下列结论正确的是( )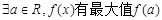
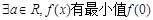
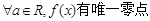
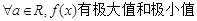
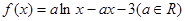 .
.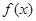 的单调区间;
的单调区间;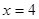 处切线的斜率为
处切线的斜率为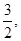 若函数
若函数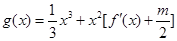 在区间(1,3)上不是单调函数,求m的取值范围.
在区间(1,3)上不是单调函数,求m的取值范围.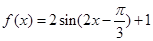 ,
, 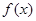 的单调递减区间;
的单调递减区间;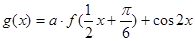 (
(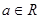 ),求函数
),求函数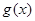 的最大值的表达式
的最大值的表达式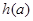 ;
;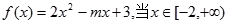 时是增函数,则m的取值范围是( )
时是增函数,则m的取值范围是( )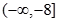
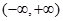
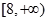
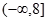
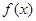 在定义域R内可导,若
在定义域R内可导,若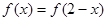 ,且当
,且当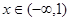 时,
时,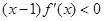 .设
.设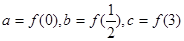 ,则( )
,则( )
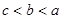
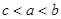
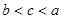
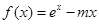 的图像为曲线C,若曲线C不存在与直线
的图像为曲线C,若曲线C不存在与直线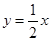 垂直的切线,则实数m的取值范围是( )
垂直的切线,则实数m的取值范围是( )