题目内容
1.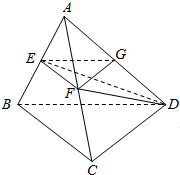 如图,在四面体ABCD中,AD=BD,∠ABC=90°,点E,F分别为棱AB,AC上的点,点G为棱AD的中点,且平面EFG∥平面BCD.求证:
如图,在四面体ABCD中,AD=BD,∠ABC=90°,点E,F分别为棱AB,AC上的点,点G为棱AD的中点,且平面EFG∥平面BCD.求证:(1)EF=$\frac{1}{2}$BC;
(2)平面EFD⊥平面ABC.
分析 (1)利用平面与平面平行的性质,可得EG∥BD,利用G为AD的中点,可得E为AB的中点,同理可得,F为AC的中点,即可证明EF=$\frac{1}{2}$BC;
(2)证明AB⊥平面EFD,即可证明平面EFD⊥平面ABC.
解答  证明:(1)因为平面EFG∥平面BCD,
证明:(1)因为平面EFG∥平面BCD,
平面ABD∩平面EFG=EG,平面ABD∩平面BCD=BD,
所以EG∥BD,…(4分)
又G为AD的中点,
故E为AB的中点,
同理可得,F为AC的中点,
所以EF=$\frac{1}{2}$BC.…(7分)
(2)因为AD=BD,
由(1)知,E为AB的中点,
所以AB⊥DE,
又∠ABC=90°,即AB⊥BC,
由(1)知,EF∥BC,所以AB⊥EF,
又DE∩EF=E,DE,EF?平面EFD,
所以AB⊥平面EFD,…(12分)
又AB?平面ABC,
故平面EFD⊥平面ABC.…(14分)
点评 本题考查平面与平面平行的性质,考查平面与平面垂直的判定,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
12.已知点P(x,y)在曲线$\left\{\begin{array}{l}x=-2+cosθ\\ y=sinθ\end{array}\right.$(θ为参数,且θ∈[π,2π))上,则点P到直线$\left\{\begin{array}{l}x=2+t\\ y=-1-t\end{array}\right.(t$为参数)的距离的取值范围是( )
| A. | [-$\frac{{3\sqrt{2}}}{2}$,$\frac{{3\sqrt{2}}}{2}$] | B. | [$\frac{{3\sqrt{2}}}{2}$-1,$\frac{{3\sqrt{2}}}{2}$+1] | C. | ($\sqrt{2}$,2$\sqrt{2}$] | D. | ($\sqrt{2}$,$\frac{{3\sqrt{2}}}{2}$+1] |
11.若平面向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-2,y)且,则$\overrightarrow{a}⊥\overrightarrow{b}$,则|$\overrightarrow{b}$|=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{2}$ | D. | 5 |