题目内容
7.设函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+2x,x<0}\\{-{x}^{2},x≥0}\end{array}\right.$,则f(1)=-1,若f(f(a))≤3,则实数a的取值范围是(-∞,$\sqrt{3}$].分析 由已知中函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+2x,x<0}\\{-{x}^{2},x≥0}\end{array}\right.$,将x=1代入,可求出f(1);再讨论f(a)的正负,代入求出f(a)≥-3,再讨论a的正负,求实数a的取值范围.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+2x,x<0}\\{-{x}^{2},x≥0}\end{array}\right.$,
∴f(1)=-12=-1,
①若f(a)<0,则f2(a)+2f(a)≤3,
解得,-3≤f(a)≤1,
即-3≤f(a)<0,
②若f(a)≥0,则-f2(a)≤3,显然成立;
则f(a)≥-3,
③若a<0,则a2+2a≥-3,
解得,a∈R,
即a<0.
④若a≥0,则-a2≥-3,
解得,0≤a≤$\sqrt{3}$,
综上所述,实数a的取值范围是:(-∞,$\sqrt{3}$].
故答案为:-1;(-∞,$\sqrt{3}$].
点评 本题考查了分段函数的应用,再已知函数值的范围时,要对自变量讨论代入函数求解,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.执行如图所示的程序框图,若输出的结果是$\frac{12}{13}$,则循环体的判断框内①处应填( )
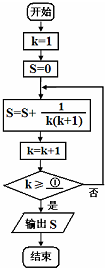

| A. | 11? | B. | 12? | C. | 13? | D. | 14? |
18.如果直线ax+by=4与圆C:x2+y2=4有两个不同的交点,那么点(a,b)和圆C的位置关系是( )
| A. | 在圆外 | B. | 在圆上 | C. | 在圆内 | D. | 不能确定 |
15.已知函数f(x)=$\frac{sinx}{|cosx|}$,则函数f(x)的最小正周期是( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
12.已知点P(x,y)在曲线$\left\{\begin{array}{l}x=-2+cosθ\\ y=sinθ\end{array}\right.$(θ为参数,且θ∈[π,2π))上,则点P到直线$\left\{\begin{array}{l}x=2+t\\ y=-1-t\end{array}\right.(t$为参数)的距离的取值范围是( )
| A. | [-$\frac{{3\sqrt{2}}}{2}$,$\frac{{3\sqrt{2}}}{2}$] | B. | [$\frac{{3\sqrt{2}}}{2}$-1,$\frac{{3\sqrt{2}}}{2}$+1] | C. | ($\sqrt{2}$,2$\sqrt{2}$] | D. | ($\sqrt{2}$,$\frac{{3\sqrt{2}}}{2}$+1] |
17. 如果图中的程序执行后输出的结果是720,那么在程序While后面的条件应为( )
如果图中的程序执行后输出的结果是720,那么在程序While后面的条件应为( )
 如果图中的程序执行后输出的结果是720,那么在程序While后面的条件应为( )
如果图中的程序执行后输出的结果是720,那么在程序While后面的条件应为( )| A. | i>8 | B. | i>7 | C. | i≥7 | D. | i≥6 |