题目内容
4.已知数列{an}满足:an+1=|an-1|,(n∈N*)(1)若a1=$\frac{11}{4}$,求a9与a10的值.
(2)若a1=a∈(k,k+1),k∈N*,求数列{an}的前3k项的和S3k(用k,a表示)
(3)是否存在a1,n0(a1∈R,n0∈N*),使得当n≥n0时,an恒为常数?若存在,求出a1,n0,若不存在,说明理由.
分析 (1)由数列an满足an+1=|an-1|(n∈N*),a1=$\frac{11}{4}$,我们分别求出a2,a3,a4,…,a9与a10;
(2)当a1=a∈(k,k+1)(k∈N*)时,易知a2=a-1,a3=a-2,…,ak=a-(k-1),利用拆项法,即可得到答案;
(3)分an≥1时,0<a1<1时,a1=b≥1时和a1=c<0时,几种情况,分别进行讨论,最后将讨论结论综合,即可得到结论.
解答 解:(1)∵a1=$\frac{11}{4}$,an+1=|an-1|,
∴a2=$\frac{7}{4}$,a3=$\frac{3}{4}$,a4=$\frac{1}{4}$,a5=$\frac{3}{4}$,
a6=$\frac{1}{4}$,a7=$\frac{3}{4}$,a8=$\frac{1}{4}$,
可得a9=$\frac{3}{4}$,a10=$\frac{1}{4}$;
(2)当a1=a∈(k,k+1)(k∈N*)时,
易知a2=a-1,a3=a-2,ak=a-(k-1),
ak+1=a-k∈(0,1),ak+2=1-ak+1=k+1-a,
ak+3=1-ak+2=a-k,ak+4=1-ak+3=k+1-a,
a3k-1=a-k,a3k=k+1-a
∴S3k=a1+a2+…+ak+ak+1+ak+2+ak+3+ak+4+…+a3k-1+a3k
=a+(a-1)+(a-2)+…+a-(k-1)+k=-$\frac{{k}^{2}}{2}$+k(a+$\frac{3}{2}$);
(3)因为存在an+1=|an-1|=$\left\{\begin{array}{l}{{a}_{n}-1,{a}_{n}≥1}\\{1-{a}_{n},{a}_{n}<1}\end{array}\right.$,
所以当an≥1时,an+1≠an
①若0<a1<1,则a2=1-a1,a3=1-a2=a1,
此时只需:a2=1-a1=a1,∴a1=$\frac{1}{2}$,
故存在a1=$\frac{1}{2}$,an=$\frac{1}{2}$,(n∈N*);
②若a1=b≥1,不妨设b∈[m,m+1),m∈N*,
易知am+1=b-m∈[0,1),
∴am+2=1-am+1=1-(b-m)=am+1=b-m,
∴b=m+$\frac{1}{2}$,∴a1=m+$\frac{1}{2}$,n≥m+1时,an=$\frac{1}{2}$,(m∈N*),
③若a1=c<0,不妨设c∈(-l,-l+1),l∈N*,易知a2=-c+1∈(l,l+1],
∴a3=a2-1=-c,al+2=-c-(l-1)∈(0,1]
∴c=-l+$\frac{1}{2}$,∴a1=-l+$\frac{1}{2}$(l∈N*),n≥l+2,则an=$\frac{1}{2}$
故存在三组a1和n0:a1=$\frac{1}{2}$时,n0=1;a1=m+$\frac{1}{2}$时,n0=m+1;
a1=-m+$\frac{1}{2}$时,n0=m+2其中m∈N*.
点评 本题考查数列递推公式及数列求和,其中正确理解数列的递推公式,并能准确的对a进行分类讨论,是解答本题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 直角三角形 | B. | 锐角三角形 | ||
| C. | 钝角三角形 | D. | 直角或钝角三角形 |
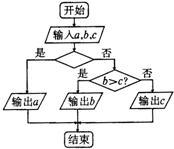
| A. | a>b? | B. | a>c? | C. | d>b或a>c? | D. | a>b且a>c? |
| A. | 13 | B. | 53 | C. | 81 | D. | 161 |