题目内容
已知双曲线 -
- =1的离心率为e,抛物线x=2py2的焦点为(e,0),则p的值为( )
=1的离心率为e,抛物线x=2py2的焦点为(e,0),则p的值为( )
| A.2 | B.1 | C. | D. |
D
解析试题分析:因为双曲线 -
- =1中a2=4,b2="12," c2=a2+b2=16,c=4,a=2,的离心率为e=
=1中a2=4,b2="12," c2=a2+b2=16,c=4,a=2,的离心率为e= ,抛物线x=2py2可知其标准方程为
,抛物线x=2py2可知其标准方程为 ,可知焦点在x轴上,且有的焦点为
,可知焦点在x轴上,且有的焦点为 ,故(e,0)=
,故(e,0)=  ,可知
,可知 ,g故选D.
,g故选D.
考点:本题主要考查了双曲线的离心率和抛物线的性质的运用。
点评:解决该试题的关键是对于标准方程中a,b的理解和表示,同时a,b,c的勾股定理也是一个易错点,非标准的方程要化为标准方程来得到。

练习册系列答案
相关题目
若椭圆 和双曲线
和双曲线 有相同的焦点
有相同的焦点 、
、 ,P是两曲线的一个公共点,则
,P是两曲线的一个公共点,则 的值是( )
的值是( )
| A.m-a | B. | C. | D. |
( )双曲线 的焦点坐标是
的焦点坐标是
A. | B. | C. | D. |
经过点P(4,-2)的抛物线标准方程为( )
| A.y2=x或x2=-8y | B.y2=x或y2=8x |
| C.y2=-8x | D.x2=-8y |
若直线 和⊙O:
和⊙O: 没有交点,则过
没有交点,则过 的直线与椭圆
的直线与椭圆 的交点个数 ( )
的交点个数 ( )
| A.至多一个 | B.0个 | C.1个 | D.2个 |
已知椭圆 和双曲线
和双曲线 ,有相同的焦点,则椭圆与双曲线的离心率的平方和为( )
,有相同的焦点,则椭圆与双曲线的离心率的平方和为( )
A. | B. | C.2 | D.3 |
若点 和点
和点 分别为椭圆
分别为椭圆 的中心和左焦点,点
的中心和左焦点,点 为椭圆上的任意一点, 则
为椭圆上的任意一点, 则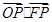 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
 的左顶点A的斜率为k的直线交椭圆C于另一个点B,且点B在x轴上的射影恰好为右焦点F,若
的左顶点A的斜率为k的直线交椭圆C于另一个点B,且点B在x轴上的射影恰好为右焦点F,若 则椭圆离心率的取值范围是( )
则椭圆离心率的取值范围是( )



 的两个焦点,过F2的直线交椭圆于点A、B,若
的两个焦点,过F2的直线交椭圆于点A、B,若 ,则
,则 ( )
( )