题目内容
若直线
和⊙O:
没有交点,则过
的直线与椭圆
的交点个数 ( )
| A．至多一个 | B．0个 | C．1个 | D．2个 |
D.
解析试题分析：因为直线和⊙O:没有交点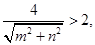,所以
所以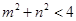
,所以点P（m,n）在内部，也在椭圆的内部，所以过的直线与椭圆相交，所以交点个数为2个.
考点：直线与圆的位置关系，直线与椭圆的位置关系，点与圆及点与椭圆的位置关系.
点评：由于直线和⊙O:没有交点,所以可得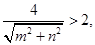
进而得到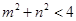,判断出点P在圆内部，也在椭圆的内部,问题到此结论确定.
练习册系列答案
名校课堂系列答案
相关题目
设
是椭圆E：
的左右焦点，P在直线
上一点，
是底角为
的等腰三角形，则椭圆E的离心率为（ ）
A． | B． | C． | D． |
双曲线
的实轴长是
| A．2 | B． | C．4 | D．4 |
已知双曲线
－
＝1的离心率为e，抛物线x＝2py2的焦点为(e,0)，则p的值为( )
| A．2 | B．1 | C． | D． |
，定义它们之间的一种“距离”：
．给出下列三个命题：
;
中，若∠C=90°，则
；
． 已知F1，F2为双曲线C：
的左右焦点，点P在C上，
，则
（ ）
| A．2 | B．4 | C． 6 | D． 8 |
已知椭圆
的长轴长为10，离心率
，则椭圆的方程是（ ）
A． 或 | B． 或 |
C． 或 | D． 或 |
抛物线
的焦点坐标是（ ）
A． | B． | C． | D． |
抛物线
截直线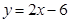
所得的弦长等于
A． | B． | C． | D．15 |