题目内容
15．若0＜α＜π，且sinα+cosα=$\frac{2}{3}$，则cosα-sinα的值是（ ）| A． | $\frac{14}{9}$ | B． | $\frac{{\sqrt{14}}}{3}$ | C． | $±\frac{{\sqrt{14}}}{3}$ | D． | $-\frac{{\sqrt{14}}}{3}$ |
分析 把已知等式两边平方，利用完全平方公式及同角三角函数间基本关系化简，整理求出2sinαcosα的值，再利用完全平方公式及同角三角函数间基本关系化简即可求出cosα-sinα的值．
解答 解：把sinα+cosα=$\frac{2}{3}$，
两边平方得：（sinα+cosα）2=1+2sinαcosα=$\frac{4}{9}$，
即2sinαcosα=-$\frac{5}{9}$，
∵0＜α＜π，
∴sinα＞0，cosα＜0，即cosα-sinα＜0，
∴（cosα-sinα）2=1-2sinαcosα=$\frac{14}{9}$，
则cosα-sinα=-$\frac{\sqrt{14}}{3}$，
故选：D．
点评 此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
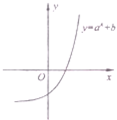函数f（x）=ax+b的图象如图，其中a，b为常数，给出下列四种说法：①a＞1，b＞0；②0＜a＜1，b＜0；③a＞1，b＞-1；④a＞1，b＜-1．则其中所有正确说法的序号是④．
按照如图所示的框图操作，