题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若
时,若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() 的图象在两点
的图象在两点![]() 处的切线分别为
处的切线分别为![]() ,若
,若![]() ,且
,且![]() ,求实数
,求实数![]() 的最小值.
的最小值.
【答案】(1)减区间是![]() ,增区间是
,增区间是![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)借助题设条件运用分类探求;(2)借助题设运用恒成立建立不等式求解;(3)依据题设构建函数,运用导数知识求解.
试题解析:
函数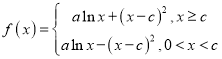 ,求导得
,求导得 ,
,
(1)当![]() 时,
时,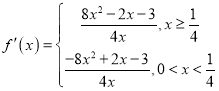 ,
,
①若![]() ,则
,则![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上单调递减;
上单调递减;
②若![]() ,则
,则![]() ,令
,令![]() ,解得
,解得![]() 或
或![]() (舍去)
(舍去)
若![]() ,则
,则![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
若![]() ,则
,则![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
综上,函数![]() 的单调减区间是
的单调减区间是![]() ,单调增区间是
,单调增区间是![]()
(2)当![]() 时,
时,![]() ,而
,而![]() ,
,
所以当![]() 时,
时,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
所以函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
所以![]() 恒成立,解得
恒成立,解得![]() 或
或![]() (舍去)
(舍去)
又由![]() ,得
,得![]() ,
,
所以实数![]() 的取值范围是
的取值范围是![]() .
.
(3)由![]() 知,
知,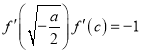 ,而
,而![]() ,则
,则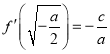 ,
,
若![]() ,则
,则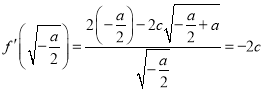 ,
,
所以![]() ,解得
,解得![]() ,不合题意
,不合题意
故![]() ,则
,则 ,
,
整理得,![]() ,
,
由![]() ,得
,得![]() ,令
,令![]() ,则
,则![]() ,
,
所以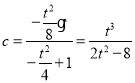 ,设
,设![]() ,则
,则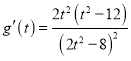 ,
,
当![]() 时,
时,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
所以函数![]() 的最小值为
的最小值为![]() ,
,
故实数![]() 的最小值为
的最小值为![]()

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
【题目】一项针对人们休闲方式的调查结果如下:受调查对象总计124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个![]() 的列联表;
的列联表;
(2)根据下列提供的独立检验临界值表,你最多能有多少把握认为性别与休闲方式有关系?
独立检验临界值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: ![]() .
.