题目内容
有10件产品,其中3件次品,7件正品,现从中抽取5件,求抽得次品件数X的分布列.
考点:离散型随机变量的期望与方差
专题:应用题,概率与统计
分析:X是取出的次品件数,取值可以是0,1,2,3,计算相应的概率,即可得到X的分布列.
解答:
解:X是取出的次品件数,取值可以是0,1,2,3,则
P(X=0)=
=
,P(X=1)=
=
,P(X=2)=
=
,P(X=3)=
=
∴X的分布列:
P(X=0)=
| ||
|
| 21 |
| 252 |
| ||||
|
| 105 |
| 252 |
| ||||
|
| 105 |
| 262 |
| ||||
|
| 21 |
| 252 |
∴X的分布列:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
点评:本题重点考查离散型随机变量的分布列,解题的关键是确定随机变量的取值,计算相应的概率.

练习册系列答案
相关题目
已知,p:A={x|y=
},q:B={x|0≤x≤2},则p是q的( )
| 2-x |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
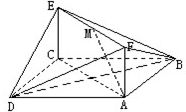 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=