题目内容
2.已知抛物线C1;x2=3y与圆C2:x2+(y-3)2=1.(1)求证:圆C2在抛物线C1内部;
(2)是否存在直线y=2x+b与圆C2和抛物线C1的从左到右的交点为A,B,C,D,使AB=CD?
(3)直线l被圆C2和抛物线C1截成长度相等的三部分,求直线l的方程.
分析 (1)在圆C2:x2+(y-3)2=1上取点P(x,y),证明P在抛物线C1内部即可;
(2)AB=CD,可得线段AD与线段BD的中点重合;
(3)利用AB=BC=CD,可得线段AD与线段BC中点重合,且AD=3BC,即可求直线l的方程.
解答 (1)证明:在圆C2:x2+(y-3)2=1上取点P(x,y),则x2=1-(y-3)2,
∴3y-x2=y2-3y+8>0,
∴P在抛物线C1内部,
∴圆C2在抛物线C1内部;
(2)解:直线y=2x+b与圆C2,联立可得5x2+4(b-3)x+(b-3)2-1=0,两根为xB,xC,
直线y=2x+b与抛物线C1,联立可得x2-6x-3b=0,两根为xA,xD,
∵AB=CD,
∴线段AD与线段BD的中点重合,
∴6=-$\frac{4(b-3)}{5}$,
∴b=-$\frac{9}{2}$
b=-$\frac{9}{2}$时,方程x2-6x-3b=0无解,
∴不存在直线y=2x+b与圆C2和抛物线C1的从左到右的交点为A,B,C,D,使AB=CD;
(3)解:设直线y=2x+b与圆C2和抛物线C1的从左到右的交点为A,B,C,D,
直线y=kx+b与圆C2,联立可得(1+k2)x2+2k(b-3)x+(b-3)2-1=0,两根为xB,xC,
直线y=kx+b与抛物线C1,联立可得x2-3kx-3b=0,两根为xA,xD,
∵AB=BC=CD,
∴线段AD与线段BC中点重合,且AD=3BC,
线段AD与线段BC中点重合,3k=-$\frac{2k(b-3)}{1+{k}^{2}}$,∴k=0或3k2=3-2b;
AD=3BC,可得(xD-xA)=3(xC-xB),
∴(xD+xA)2-4xDxA=9[(xC+xB)2-4xCxB],
k=0时,12b=-36[(b-3)2-1],∴b=3或b=$\frac{8}{3}$;
3k2=3-2b时,b<$\frac{3}{2}$,△=4k2(b-3)2-4(k2+1)[(b-3)2-1]=4(3-b)(2b-7)<0无解,
∴所求直线l的方程为y=3或y=$\frac{8}{3}$.
点评 本题考查圆与抛物线的综合,考查直线与圆、直线与抛物线的位置关系,考查学生分析解决问题的能力,有难度.

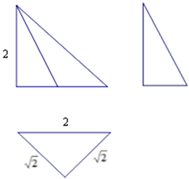 一个几何体的三视图如图.该几何体的各个顶点都在球O的球面上,球O的体积为( )
一个几何体的三视图如图.该几何体的各个顶点都在球O的球面上,球O的体积为( )| A. | $\frac{\sqrt{2}}{3}$π | B. | $\frac{4\sqrt{2}}{3}$π | C. | $\frac{8\sqrt{2}}{3}$π | D. | $\frac{10\sqrt{2}}{3}$π |
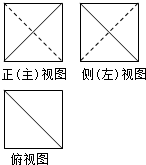 一个边长为2的正方体截去两个角后所得几何体的三视图如图所示,则该几何体的体积为( )
一个边长为2的正方体截去两个角后所得几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{8}{3}$ | B. | $\frac{16}{3}$ | C. | 6 | D. | $\frac{20}{3}$ |
| A. | {-2.5}∉Z | B. | ∅⊆{x|x<-3} | C. | {a}∈{a、b、c} | D. | 1⊆{1} |