题目内容
14.(1)已知△ABC的3内角为A、B、C,求证:sin2A=sin2B+sin2C-2sinB•sinC•cosA.(2)若α+β=$\frac{2π}{3}$,且α>0,β>0,根据(1)的结论求sin2α+sin2β-sinαsinβ的值.
分析 (1)△ABC中,利用余弦定理可得a2+b2-c2=2ab•cosC.再利用正弦定理可得sin2A+sin2B-sin2C=2sinAsinBcosC,可得要证的等式成立.
(2)由α+β$+\frac{π}{3}$=π,根据结论(1)可得:sin2$\frac{π}{3}$=sin2α+sin2β-2sinα•sinβ•cos$\frac{π}{3}$,利用特殊角的三角函数值即可得解.
解答 解:(1)证明:△ABC中,利用余弦定理可得cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$,
即b2+c2-a2=2bc•cosA.
再利用正弦定理可得sin2B+sin2C-sin2A=2sinCsinBcosA,
∴sin2A=sin2B+sin2C-2sinB•sinC•cosA.得证.
(2)∵α+β$+\frac{π}{3}$=π,
∴由(1)可得:sin2$\frac{π}{3}$=sin2α+sin2β-2sinα•sinβ•cos$\frac{π}{3}$.
∴可得:$\frac{3}{4}$=sin2α+sin2β-sinα•sinβ.
点评 此题考查了正弦、余弦定理,熟练掌握余弦定理是解本题的关键,属于基本知识的考查.

练习册系列答案
相关题目
9.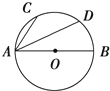 如图,已知AB是圆O的直径,点C、D是半圆弧的两个三等分点,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=( )
如图,已知AB是圆O的直径,点C、D是半圆弧的两个三等分点,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=( )
 如图,已知AB是圆O的直径,点C、D是半圆弧的两个三等分点,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=( )
如图,已知AB是圆O的直径,点C、D是半圆弧的两个三等分点,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=( )| A. | $\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$ | C. | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | D. | $\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ |
19.已知三次函数f(x)=(x-1)(x-2)(x-a)(1<a<2),则$\frac{1}{f′(1)}$+$\frac{4}{f′(2)}$+$\frac{{a}^{2}}{f′(a)}$=1.
4.若x1是Ax=b的解,x2是Ax=0的解,则( )是Ax=b的解(k为任意常数)
| A. | kx1+x2 | B. | kx1+kx2 | C. | kx1-kx2 | D. | x1+kx2 |