题目内容
已知直线ax-by-2=0与曲线y=x3-lnx在点p(1,1)处的切线互相垂直,则
为______.
| a |
| b |
曲线y=x3-lnx的导数为f′(x)=3x2-
,则当x=1时,f'(1)=3-1=2,即切线的斜率k=2,
因为直线ax-by-2=0点p(1,1)处的切线互相垂直,所以直线ax-by-2=0为-
.
即
=-
,所以
=-2.
故答案为:-2.
| 1 |
| x |
因为直线ax-by-2=0点p(1,1)处的切线互相垂直,所以直线ax-by-2=0为-
| 1 |
| 2 |
即
| a |
| b |
| 1 |
| 2 |
| a |
| b |
故答案为:-2.

练习册系列答案
相关题目
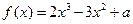 的极大值为
的极大值为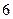 ,则
,则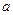 等于( )
等于( )