题目内容
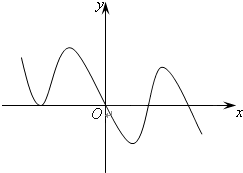
设a∈R，若函数y=x3+ax，x∈R有大于零的极值点，则（ ）
| A．a＞0 | B．a＜0 | C．a≥0 | D．a≤0 |
∵函数y=x3+ax，x∈R有大于零的极值点，
∴f（x）的导数 f′（x）=3x2+a=0有大于0的实根，
∴a＜0，
故选 B．
∴f（x）的导数 f′（x）=3x2+a=0有大于0的实根，
∴a＜0，
故选 B．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
，
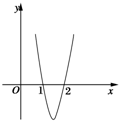
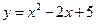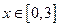的值域。