题目内容
【题目】已知函数![]() ,
,![]() 的最小正期为
的最小正期为![]() .
.
(1)求![]() 的单调增区间;
的单调增区间;
(2)方程![]() 在
在![]() 上有且只有一个解,求实数
上有且只有一个解,求实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() 满足对任意
满足对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立.若存在,求
成立.若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
(1)利用降幂公式和辅助角公式化简得![]() ,再利用周期公式求得
,再利用周期公式求得![]() 的值,从而得到
的值,从而得到![]() 的解析式,再利用整体代入求单调区间;
的解析式,再利用整体代入求单调区间;
(2)方程![]() ;在
;在![]() 上有且有一个解,转化为函数
上有且有一个解,转化为函数![]() 与函数
与函数![]() 只有一个交点;
只有一个交点;
(3)由(1)可知![]() ,则
,则![]() ;实数
;实数![]() 满足对任意
满足对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,即
成立,即![]() 成立,再将问题转化为恒成立问题.
成立,再将问题转化为恒成立问题.
(1)函数![]()
∵![]() 的最小正周期为
的最小正周期为![]() .
.![]() ∴
∴![]() ,∴
,∴![]() .
.
那么![]() 的解析式
的解析式![]()
令![]() 得:
得:![]()
∴![]() 的单调增区间为
的单调增区间为![]() .
.
(2)方程![]() ;在
;在![]() 上有且有一个解,
上有且有一个解,
转化为函数![]() 与函数
与函数![]() 只有一个交点.
只有一个交点.
∵![]() ,∴
,∴![]()
因为函数![]() 在
在![]() 上增,在
上增,在![]() 上减,
上减,
且![]() ,
,
∴![]() 或
或![]() ,所以
,所以![]() 或
或![]() .
.
(3)由(1)可知![]() ,∴
,∴![]() .
.
实数![]() 满足对任意
满足对任意![]() ,都存在
,都存在![]() ,
,
使得![]() 成立.
成立.
即![]() 成立
成立
令![]()
设![]() ,那么
,那么![]()
∵![]() ,∴
,∴![]() ,
,
可得![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,其对称轴
,其对称轴![]() ,
,
∵![]() 上,
上,
∴①当![]() 时,即
时,即![]() ,
,![]() ,解得
,解得![]() ;
;
②当![]() ,即
,即![]() 时,
时,![]() ,解得
,解得![]() ;
;
③当![]() ,即
,即![]() 时,
时,![]() ,解得
,解得![]() ;
;
综上可得,存在![]() ,可知
,可知![]() 的取值范围是
的取值范围是![]() .
.

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案【题目】为了调查某社区居民每天参加健身的时间,某机构在该社区随机采访男性、女性各50名,其中每人每天的健身时间不少于1小时称为“健身族”,否则称其为"非健身族”,调查结果如下:
健身族 | 非健身族 | 合计 | |
男性 | 40 | 10 | 50 |
女性 | 30 | 20 | 50 |
合计 | 70 | 30 | 100 |
(1)若居民每人每天的平均健身时间不低于70分钟,则称该社区为“健身社区”. 已知被随机采访的男性健身族,男性非健身族,女性健身族,女性非健身族每人每天的平均健分时间分別是1.2小时,0.8小时,1.5小时,0.7小时,试估计该社区可否称为“健身社区”?
(2)根据以上数据,能否在犯错误的概率不超过5%的情况下认为“健身族”与“性别”有关?
参考公式: 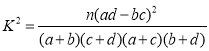 ,其中
,其中![]() .
.
参考数据:
| 0. 50 | 0. 40 | 0. 25 | 0. 05 | 0. 025 | 0. 010 |
| 0. 455 | 0. 708 | 1. 321 | 3. 840 | 5. 024 | 6. 635 |

