Question

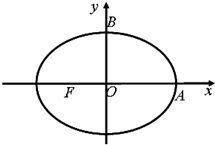
如图，点F是椭圆W：

x2

a2

+

y2

b2

=1(a＞b＞0)的左焦点，A、B分别是椭圆的右顶点与上顶点，椭圆的离心率为

1

2

，三角形ABF的面积为

3 3

2

，
（Ⅰ）求椭圆W的方程；
（Ⅱ）对于x轴上的点P（t，0），椭圆W上存在点Q，使得PQ⊥AQ，求实数t的取值范围；
（Ⅲ）直线l：y=kx+m（k≠0）与椭圆W交于不同的两点M、N（M、N异于椭圆的左右顶点），若以MN为直径的圆过椭圆W的右顶点A，求证：直线l过定点，并求出该定点的坐标．

Answer 1

（Ⅰ）由e=

c

a

=

1

2

，即a=2c，得b=

a2-c2

=

3

c，
∴S△ABF=

1

2

(a+c)•b=

3 3

2

c2=

3 3

2

，解得c²=1，∴a²=4c²=4，b²=a²-c²=3，
∴椭圆W的方程为

x2

4

+

y2

3

=1；…（3分）
（Ⅱ）A（2，0），P（t，0），设Q（x，y），则

x2

4

+

y2

3

=1，

PQ

=(x-t，y)，

AQ

=(x-2，y)，
∵

PQ

⊥

AQ

，∴（x-t）（x-2）+y²=0，∴(x-t)(x-2)+3(1-

x2

4

)=0，…（5分）
∵-2＜x＜2，∴x-t-

3(2+x)

4

=0，即t=

x-6

4

∈(-2，-1)；…（7分）
（Ⅲ）证明：联立

y=kx+m 3x2+4y2=12

消y得：（3+4k²）x²+8kmx+4m²-12=0，
设M（x₁，y₁），N（x₂，y₂），△=（8km）²-4（3+4k²）（4m²-12）＞0，即m²＜3+4k²，x1+x2=-

8km

3+4k2

，x1x2=

4m2-12

3+4k2

，…（9分）

AM

=(x1-2，y1)，

AN

=(x2-2，y2)，
若以MN为直径的圆过椭圆W的右顶点A，则

AM

•

AN

=(x1-2)(x2-2)+y1y2=0，
即（x₁-2）（x₂-2）+（kx₁+m）（kx₂+m）=0，…（11分）
展开整理得：x1x2-2(x1+x2)+4+k2x1x2+km(x1+x2)+m2=0，
即

4m2-12

3+4k2

-2(-

8km

3+4k2

)+4+k2(

4m2-12

3+4k2

)+km(-

8km

3+4k2

)+m2=0，
通分化简得

7m2+16km+4k2

3+4k2

=0，即7m²+16km+4k²=0，
分解得（7m+2k）（m+2k）=0，得7m+2k=0或m+2k=0，即m=-

2k

7

或m=-2k，
当m=-

2k

7

时，直线y=kx+m=k(x-

2

7

)，即直线过定点(

2

7

，0)
当m=-2k时，直线y=kx+m=k（x-2），即直线过定点（2，0），但与右顶点A重合，舍去，
综合知：直线l过定点，该定点的坐标为(

2

7

，0)．…（14分）