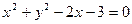题目内容
已知实数x、y满足方程x2+y2-4x+1=0.求
(1) 的最大值和最小值;(2)y-x的最小值;(3)x2+y2的最大值和最小值.
的最大值和最小值;(2)y-x的最小值;(3)x2+y2的最大值和最小值.
(1)
 的最大值和最小值;(2)y-x的最小值;(3)x2+y2的最大值和最小值.
的最大值和最小值;(2)y-x的最小值;(3)x2+y2的最大值和最小值.(1)kmax= ,kmin=-
,kmin=- . (2)(y-x)min=-2-
. (2)(y-x)min=-2-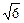 .
.
(3)2-
 ,kmin=-
,kmin=- . (2)(y-x)min=-2-
. (2)(y-x)min=-2-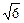 .
.(3)2-

(1)如图,方程x2+y2-4x+1=0表示以点(2,0)为圆心,以 为半径的圆.
为半径的圆.
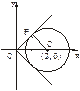
设 =k,即y=kx,由圆心(2,0)到y=kx的距离为半径时直线与圆相切,斜率取得最大、最小值.由
=k,即y=kx,由圆心(2,0)到y=kx的距离为半径时直线与圆相切,斜率取得最大、最小值.由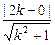 =
= ,解得k2=3.所以kmax=
,解得k2=3.所以kmax= ,kmin=-
,kmin=- .
.
(也可由平面几何知识,有OC=2,OP= ,∠POC=60°,直线OP的倾斜角为60°,直线OP′的倾斜角为120°解之)
,∠POC=60°,直线OP的倾斜角为60°,直线OP′的倾斜角为120°解之)
(2)设y-x=b,则y=x+b,仅当直线y=x+b与圆切于第四象限时,纵轴截距b取最小值.由点到直线的距离公式,得
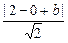 =
= ,即b=-2±
,即b=-2±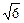 ,故(y-x)min=-2-
,故(y-x)min=-2-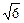 .
.
(3)x2+y2是圆上点与原点距离之平方,故连结OC,与圆交于B点,并延长交圆于C′,则(x2+y2)max=|OC′|=2+ ,(x2+y2)min=|OB|=2-
,(x2+y2)min=|OB|=2- .
.
 为半径的圆.
为半径的圆.
设
 =k,即y=kx,由圆心(2,0)到y=kx的距离为半径时直线与圆相切,斜率取得最大、最小值.由
=k,即y=kx,由圆心(2,0)到y=kx的距离为半径时直线与圆相切,斜率取得最大、最小值.由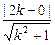 =
= ,解得k2=3.所以kmax=
,解得k2=3.所以kmax= ,kmin=-
,kmin=- .
.(也可由平面几何知识,有OC=2,OP=
 ,∠POC=60°,直线OP的倾斜角为60°,直线OP′的倾斜角为120°解之)
,∠POC=60°,直线OP的倾斜角为60°,直线OP′的倾斜角为120°解之)(2)设y-x=b,则y=x+b,仅当直线y=x+b与圆切于第四象限时,纵轴截距b取最小值.由点到直线的距离公式,得
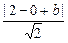 =
= ,即b=-2±
,即b=-2±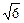 ,故(y-x)min=-2-
,故(y-x)min=-2-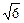 .
.(3)x2+y2是圆上点与原点距离之平方,故连结OC,与圆交于B点,并延长交圆于C′,则(x2+y2)max=|OC′|=2+
 ,(x2+y2)min=|OB|=2-
,(x2+y2)min=|OB|=2- .
.
练习册系列答案
相关题目
 轴上两个截距分别为
轴上两个截距分别为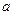 ,
,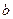 ,在
,在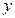 轴上的一个截距为
轴上的一个截距为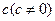 ,试求此圆方程.
,试求此圆方程.
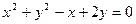
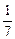 B.-1<t<
B.-1<t< C.-
C.-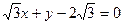 截圆
截圆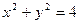 得的劣弧所对的圆心角为( )
得的劣弧所对的圆心角为( )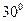
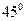
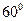
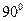
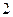 ,圆心在
,圆心在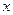 轴的正半轴上,直线
轴的正半轴上,直线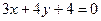 与圆C相切,
与圆C相切,