题目内容
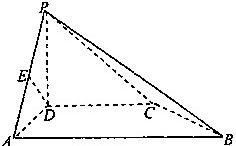
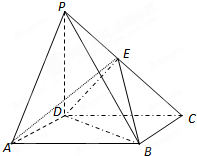
如图所示,PD⊥底面ABCD,四边形ABCD是正方形,PD=DC,E是PC的中点.
(1)证明:PA∥平面BDE;
(2)证明:平面ADE⊥平面PBC;
(3)求直线AE与平面ABCD所成角的余弦值.
(1)证明:PA∥平面BDE;
(2)证明:平面ADE⊥平面PBC;
(3)求直线AE与平面ABCD所成角的余弦值.

(1)连接AC,交BD于O,连接EO.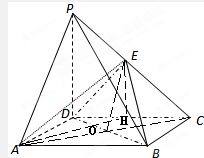
∵四边形ABCD是正方形,∴O为AC中点,
∵△PAC中,E为PA的中点,
∴OE是△PAC的中位线,可得OE∥PA.
又∵OE?平面BDE,PA?平面BDE,
∴PA∥平面BDE;
(2)∵PD⊥平面ABCD,BC?平面ABCD,
∴PD⊥BC
又∵CD⊥BC,PD、CD是平面PCD内的相交直线
∴BC⊥平面PCD,结合DE?平面PCD,得DE⊥BC,
∵△PCD中,PD=DC,E为P中点,∴DE⊥PC,
∵PC、BC是平面PBC内的相交直线
∴DE⊥平面PBC
∵DE?平面ADE,∴平面ADE⊥平面PBC;
(3)取CD中点,连接AH、EH
∵△PCD中,E、H分别为PC、CD的中点
∴EH∥PD,结合PD⊥平面ABCD,可得EH⊥平面ABCD
因此,AH就是AE在平面BACD内的射影
∴∠EAH就是直线AE与平面ABCD所成角
∵Rt△AEH中,AH=
=
,EH=
PD=1
∴AE=
=
,可得cos∠EAH=
=
即直线AE与平面ABCD所成角的余弦值为

∵四边形ABCD是正方形,∴O为AC中点,
∵△PAC中,E为PA的中点,
∴OE是△PAC的中位线,可得OE∥PA.
又∵OE?平面BDE,PA?平面BDE,
∴PA∥平面BDE;
(2)∵PD⊥平面ABCD,BC?平面ABCD,
∴PD⊥BC
又∵CD⊥BC,PD、CD是平面PCD内的相交直线
∴BC⊥平面PCD,结合DE?平面PCD,得DE⊥BC,
∵△PCD中,PD=DC,E为P中点,∴DE⊥PC,
∵PC、BC是平面PBC内的相交直线
∴DE⊥平面PBC
∵DE?平面ADE,∴平面ADE⊥平面PBC;
(3)取CD中点,连接AH、EH
∵△PCD中,E、H分别为PC、CD的中点
∴EH∥PD,结合PD⊥平面ABCD,可得EH⊥平面ABCD
因此,AH就是AE在平面BACD内的射影
∴∠EAH就是直线AE与平面ABCD所成角
∵Rt△AEH中,AH=
| AD2+DH2 |
| 5 |
| 1 |
| 2 |
∴AE=
| AH2+EH2 |
| 6 |
| AH |
| AE |
| ||
| 6 |
即直线AE与平面ABCD所成角的余弦值为
| ||
| 6 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目