题目内容
【题目】已知![]() 为抛物线
为抛物线![]() :
:![]() 的焦点,过
的焦点,过![]() 的动直线交抛物线
的动直线交抛物线![]() 于
于![]() ,
,![]() 两点.当直线与
两点.当直线与![]() 轴垂直时,
轴垂直时,![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)设直线![]() 的斜率为1且与抛物线的准线
的斜率为1且与抛物线的准线![]() 相交于点
相交于点![]() ,抛物线
,抛物线![]() 上存在点
上存在点![]() 使得直线
使得直线![]() ,
,![]() ,
,![]() 的斜率成等差数列,求点
的斜率成等差数列,求点![]() 的坐标.
的坐标.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)由题意可得![]() ,即可求出抛物线的方程,(2)设直线
,即可求出抛物线的方程,(2)设直线![]() 的方程为
的方程为![]() ,联立
,联立![]() 消去
消去![]() ,得
,得![]() ,根据韦达定理结合直线
,根据韦达定理结合直线![]() ,
,![]() ,
,![]() 的斜率成等差数列,即可求出点
的斜率成等差数列,即可求出点![]() 的坐标.
的坐标.
解:(1)因为![]() ,在抛物线方程
,在抛物线方程![]() 中,令
中,令![]() ,可得
,可得![]() .
.
于是当直线与![]() 轴垂直时,
轴垂直时,![]() ,解得
,解得![]() .
.
所以抛物线的方程为![]() .
.
(2)因为抛物线![]() 的准线方程为
的准线方程为![]() ,所以
,所以![]() .
.
设直线![]() 的方程为
的方程为![]() ,
,
联立![]() 消去
消去![]() ,得
,得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
若点![]() 满足条件,则
满足条件,则![]() ,
,
即![]() ,
,
因为点![]() ,
,![]() ,
,![]() 均在抛物线上,所以
均在抛物线上,所以![]() ,
,![]() ,
,![]() .
.
代入化简可得![]() ,
,
将![]() ,
,![]() 代入,解得
代入,解得![]() .
.
将![]() 代入抛物线方程,可得
代入抛物线方程,可得![]() .
.
于是点![]() 为满足题意的点.
为满足题意的点.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案【题目】随着科技的发展,网购已经逐渐融入了人们的生活.在家里面不用出门就可以买到自己想要的东西,在网上付款即可,两三天就会送到自己的家门口,如果近的话当天买当天就能送到,或者第二天就能送到,所以网购是非常方便的购物方式.某公司组织统计了近五年来该公司网购的人数![]() (单位:人)与时间
(单位:人)与时间![]() (单位:年)的数据,列表如下:
(单位:年)的数据,列表如下:
| 1 | 2 | 3 | 4 | 5 |
| 24 | 27 | 41 | 64 | 79 |
(1)依据表中给出的数据,是否可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(计算结果精确到0.01).(若
并加以说明(计算结果精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式
 ,参考数据
,参考数据![]() .
.
(2)建立![]() 关于
关于![]() 的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
(参考公式:
 ,
,![]() )
)
【题目】随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到表(单位:人)
经常网购 | 偶尔或不用网购 | 合计 | |
男性 | 50 | 100 | |
女性 | 70 | 100 | |
合计 |
(1)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关?
(2)①现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
②将频率视为概率,从我市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为![]() ,求随机变量
,求随机变量![]() 的数学期望和方差.
的数学期望和方差.
参考公式: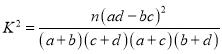
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |